最近看了一些微电网优化调度的论文，苦于无从下手之际，看到一道微电网日前优化调度相关的数学建模题；题目提供了一个简单的风光储微电网场景及测试数据，正好拿来练手。本文基于Python第三方库实现题目的混合整数规划模型，并使用默认的求解器求解。输入数据及汇总代码，参见文末。

问题出自第十届“中国电机工程学会杯”全国大学生电工数学建模竞赛A题：微电网日前优化调度。

下图示意了一个含有风机、光伏、蓄电池及常见负荷的微电网系统。日前经济调度问题是指在对风机出力、光伏出力、常规负荷进行日前（未来24h）预测的基础上，考虑电网测的分时电价，充分利用微网中的蓄电池等可调控手段，使微电网运行的经济性最优。

题目要求在如下已知条件下，求不同调度方案的平均用电成本：

• 未来24h、每隔15min共96个时间点的负荷、光伏、风机出力预测，及分时电价数据；

• 风机容量250kW，发电成本0.52元/kWh；

• 光伏容量150kW，发电成本0.75元/kWh；

• 蓄电池容量300kWh；SOC初始值0.4，运行范围[0.3, 0.95]；由充电至放电成为为0.2元/kWh；日充放电次数限制均为8；忽略蓄电池损耗；

完整问题描述参考：

• 第十届“中国电机工程学会杯”全国大学生电工数学建模竞赛 A 题：微电网日前优化调度
• 微电网日前优化调度 。算例有代码（0）

题目涉及电网、新能源（风机、光伏）、蓄电池及负荷四类资源，我们依次建立其线性规划模型，然后交给求解器求解。一个线性规划模型包含：

• 设计变量：各类资源的实时出力数据
• 约束条件：能量平衡及各类资源应该满足的技术参数，例如蓄电池的容量限制、SOC限制、充放电次数限制等
• 目标函数：运行成本，具体到本题即用电成本

本文基于 Python 第三方库实现。是一个线性规划问题建模库，将数学模型转换为 MPS 或者 LP 文件，然后调用 LP 求解器如 CBC、GLPK、CPLEX、Gurobi 等求解。具体用法参考下面链接，本文不再赘述。

• PuLP Documentation
• Python求解线性规划——PuLP使用教程

开始之前先抽象一个模型基类，表示各类调度设备，包含名称、容量、使用成本等基本属性，同时提供一个方法，用于实现设计变量、约束条件、目标函数等线性规划模型三要素。模型求解后，调用属性获取变量值，即每个时刻的出力。

接下来依次建立电网、新能源（风机、光伏）及蓄电池的模型。

(1) 电网模型

电网模型继承自基类，同时新增了 卖电收益 属性，并且满足容量约束即每个时刻的出力不能超过限定值，目标函数为运行成本即用电费用与卖电收益的差值。

直观地，任意时刻可以用一个变量 $p^i$ 来表示电网的出力：正值表示从电网买电，或者负值表示卖电给电网。但是，事先并不知道 $p^i$ 的正负，也就没法计算此刻的运行成本（不能将线性规划变量直接用于语句中）。因此，引入买电、卖电两个中间变量来分开描述：

• $p_f^i\ge 0$ 表示 $i$ 时刻从电网买电量；
• $p_t^i\ge 0$ 表示 $i$ 时刻向电网卖电量；

因为同一时刻电流只能单向流动，即 $p_f^i$ 和 $p_t^i$ 至少有一个等于0：$p_f^i?p_t^i=0$。

但这并不是一个合法的线性约束，需要再引入一个变量：

• $b_i=\{0，1\}$：1 表示从电网买电即 $p_t^i=0$，0 表示卖电到电网即 $p_f^i=0$

于是线性约束表示为：

$$\begin{gathered} 0\le p_f^i\le b^i?C \\ 0\le p_t^i\le (1?b^i)?C \end{gathered}$$

其中，$C$为电网容量（交换功率）限制值。

最终，电网 $i$ 时刻实际出力 $p^i$ 及用电成本（买电或卖电）$c^i$：

$$\begin{gathered} p^i=p_f^i?p_t^i \\ {c}^i=p_f^i?u_1?dt?p_t^i?u_2?dt \end{gathered}$$

其中，$u_1,u_2$分别为该时刻单位买电成本、卖电收益（元/kWh），$dt$ 为时间步长。

(2) 新能源发电模型

将风机和光伏抽象为新能源发电模型，约束条件为 每一时刻的电力供应不大于预测出力，如果不允许弃风弃光的话，则等于预测出力值。因此，在类基础上增加两个输入参数：

• ：每一时刻的出力预测，即一个列向量/数组/时间序列；
• ：是否允许弃风弃光，默认允许。

相应地，提供一个输出属性表示新能源发电的实际利用率。

(3) 蓄电池模型

原题已经给出了蓄电池的混合整数规划数学模型，除了基类中的容量、单位用电成本外，还有如下主要参数：

• ：爬坡限制值，即原题公式（5）中的数值 20%
• ：初始SOC状态
• ：电量范围SOC限制
• ：充放电次数限制

参考原题的约束：

• 爬坡约束：公式（3）（5）
• 容量约束：公式（1）（2）
• 调度周期始末电量相等：公式（4）
• 充放电次数约束：公式（6）

类比上文对电网买电、卖电行为的建模，同一时刻也需要三个中间变量：充电功率 $p_c^i$、放电功率 $p_d^i$、充放电状态 $b^i$ （1-放电，0-充电）来描述电池的出力。前三个约束的实现不再赘述，下面重点解析充放电次数约束。

充放电状态序列 $b=\{b^1,b^2,...,b^n\}$，引入辅助的变量 $t$ 表示相邻状态相减的绝对值，即

$$t^i=|b^{i+1}?b^i|1=1,2,3,...,n?1$$

当 $t^i=1$ 时，即相邻的充放电状态由0变成了1，或者由1变成了0，表示完成了一次充放电周期。于是总的充放电次数限制约束可以表示为：

$$\Sigma t^i\le N_c$$

那么如何将含有绝对值的等式 $t^i=|b^{i+1}?b^i|$ 变换为线性约束呢？结合本文场景，将等式松弛一下 $t^i\ge |b^{i+1}?b^i|$：

• $t^i=1$ 正是我们需要计数的情况；
• $t^i=0$ 没有增加计数，此时 $b^{i+1}=b^i$ 表明并未发生充放电状态变化，恰好可以对应上。

于是，上述绝对值等式约束等效为：

$$?t^i\le b^{i+1}?b^i\le t^i$$

(4) 风光储优化调度模型

最后，我们抽象出一个微电网类，包含上述能源设备及负荷，同时引入系统能量平衡约束，建立最终的优化模型。其中的几个方法：

• ：建模和求解过程
• ：目标函数值即总用电费用
• ：平均用电成本

本节根据上文建立的优化调度模型，求解提问中的不同调度策略。

先导入全天96个时刻的时间序列数据：

(1) 经济性评估方案

问题：微网中蓄电池不作用，微网与电网交换功率无约束，无可再生能源情况下，分别计算各时段负荷的供电构成（kW）、全天总供电费用(元)和负荷平均购电单价（元/kWh）。

这一问不用优化模型也能解，多余的电卖给电网、不足的电从电网购买即可，参考这篇文章的解析过程。但既然我们已经建立了统一的优化调度模型，本例只要引入电网一种资源，将其作为一个特例直接求解即可。

因为电网交换功率没有限制，直接设一个较大的数例如$10^6$即可。

输出：

问题：微网中蓄电池不作用，微网与电网交换功率无约束，可再生能源全额利用情况下，分别计算各时段负荷的供电构成（kW）、全天总供电费用(元)和负荷平均购电单价（元/kWh）。

这一问将风机和光伏加入微网，同时注意设置不可弃风弃光（可再生能源全额利用）。

输出：

因为限定全额利用可再生能源，所以弃风弃光率都是0。风机、光伏的用电成本较高，即便可以将风机、光伏的电卖给电网，其最终收益还不如低电价时刻从电网直接买电，所以全额利用可再生能源情况下，这一小问的平均用电成本高于上一问的纯网电。

(2) 最优日前调度方案一

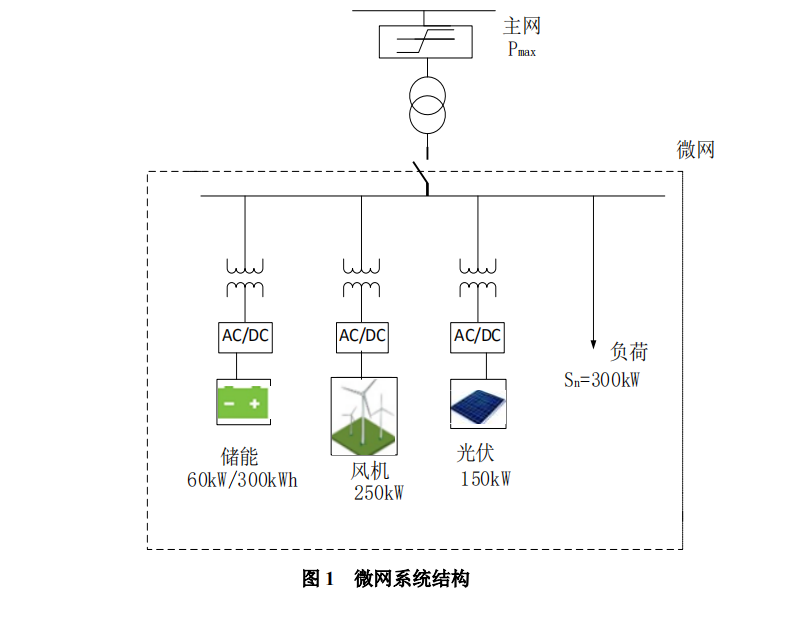
问题：不计蓄电池作用，微网与电网交换功率无约束，以平均负荷供电单价最小为目标（允许弃风弃光），分别计算各时段负荷的供电构成（kW）、全天总供电费用(元)和平均购电单价（元/kWh），分析可再生能源的利用情况。

这个调度方案是在上一问的基础上允许弃风弃光，即合理选择使用新能源发电还是网电。同样，我们设置输入参数，然后交给优化模型即可。注意和上一段代码的唯一区别是设置允许弃风弃光 。

输出：

因为可以根据经济最优选择合适的电力来源，这一调度方案的平均用电成本低于前两问。例如，凌晨时段网电电价本来就低，所以选择直接弃掉此时的风机和光伏电力（参见弃风弃光率）；网电峰电时段择机考虑风电和光伏。这篇文章 从电价解析的角度分析了这个问题，人为分析的策略与本文优化的结果很接近，可以作为参考。

(3) 最优日前调度方案二

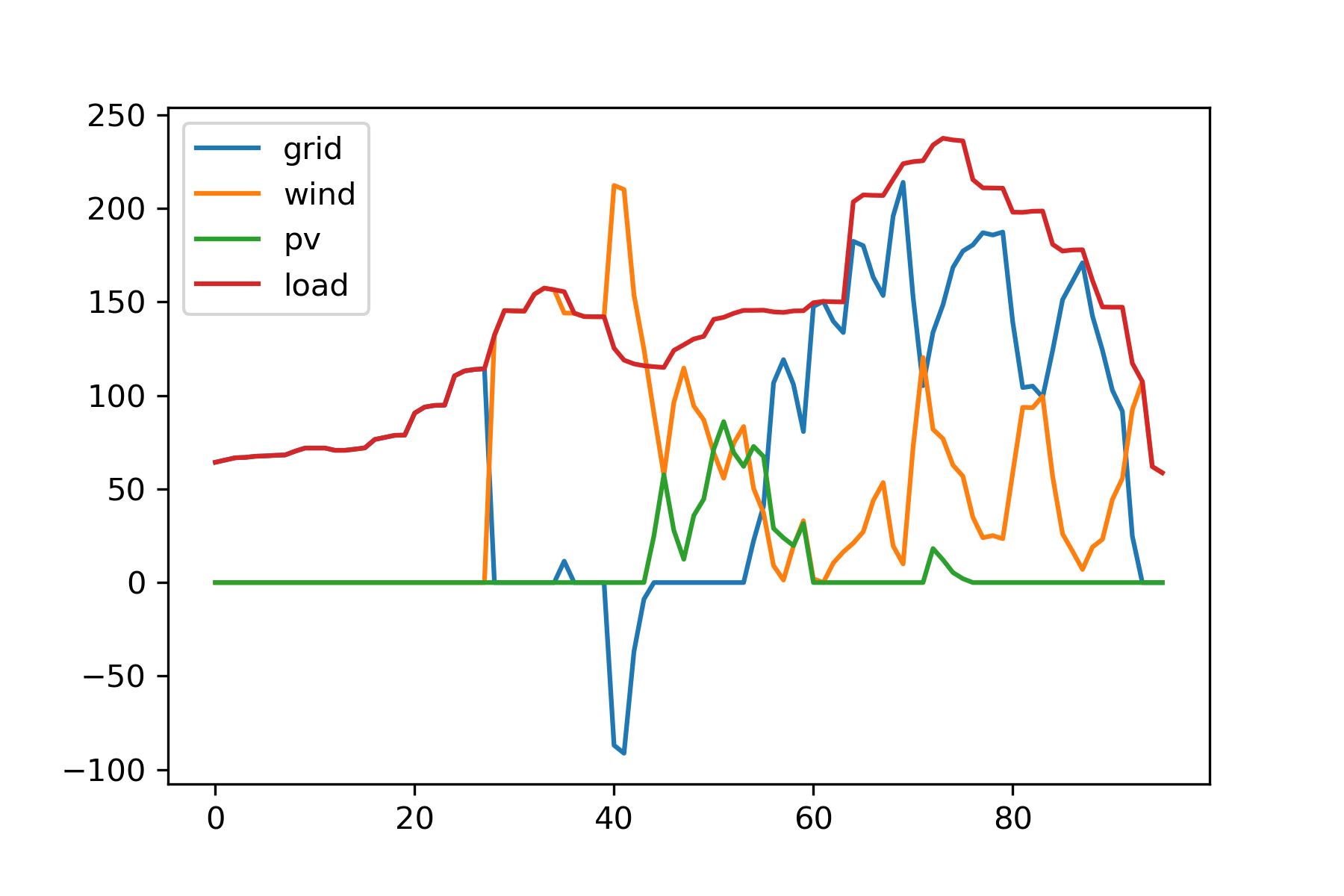
问题：考虑蓄电池作用，且微网与电网允许交换功率不超过150kW，在可再生能源全额利用的条件下，以负荷平均供电单价最小为目标，建立优化模型，给出最优调度方案，包括各时段负荷的供电构成（kW）、全天总供电费用(元)和平均购电单价（元/kWh），分析蓄电池参与调节后产生的影响。

这个调度方案在基础场景（1）第二问的基础上引入了蓄电池，同时限制了电网交换功率。

输出：

相比基础场景（1）第二问的平均用电成本0.6879，本方案用电成本有所降低。结合下图具体调度可知，蓄电池将凌晨高成本的新能源电力转移到了网电的峰电时段，因此比直接在凌晨时段卖高成本的新能源电力更为划算。这篇文章也解答了本问题，可以作为参考。

(4) 最优日前调度方案三

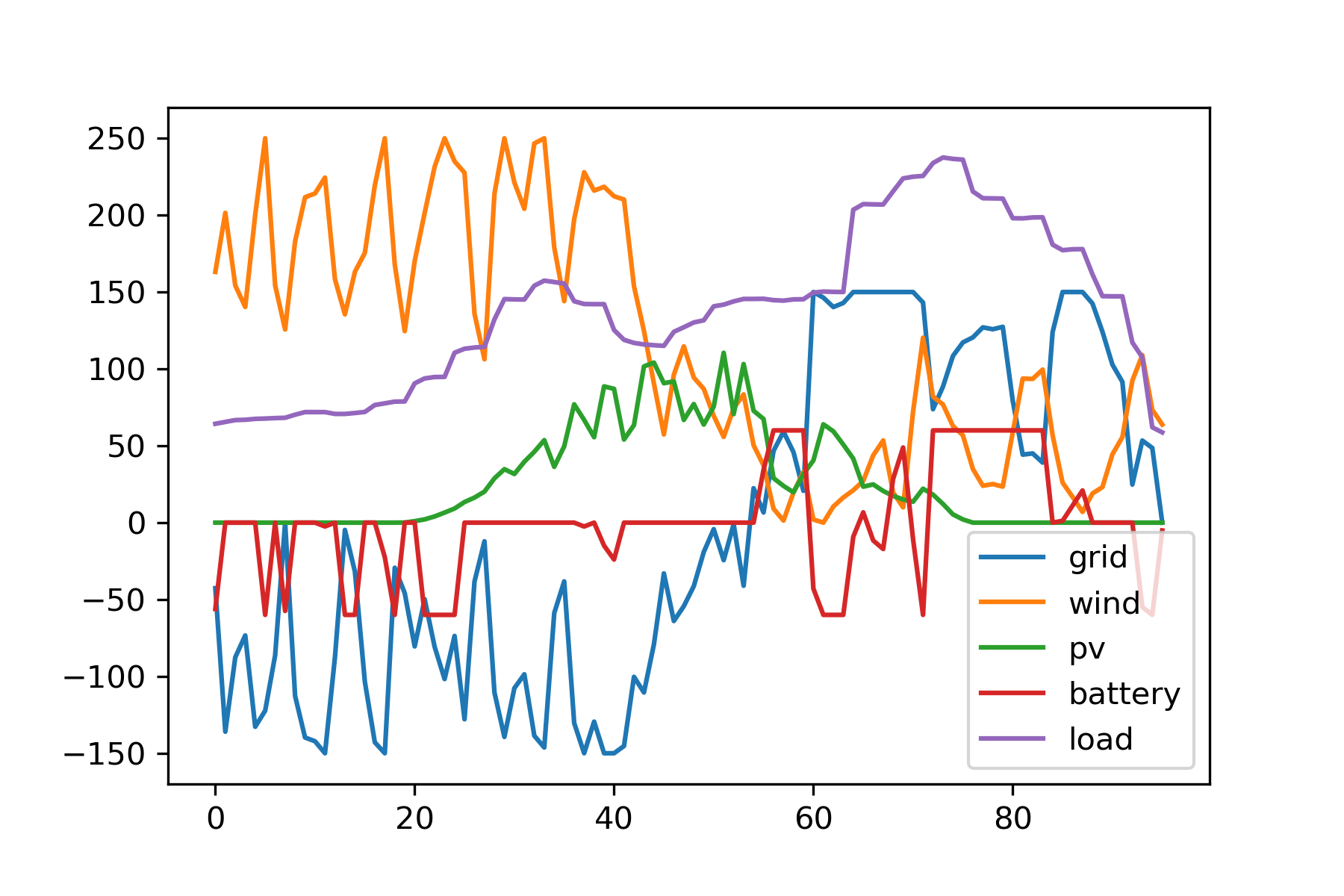
问题：考虑蓄电池作用，且微网与电网允许交换功率不超过150kW，以负荷供电成本最小为目标（允许弃风弃光），建立优化模型，给出最优调度方案，包括各时段负荷的供电构成（kW）、全天总供电费用(元)和平均购电单价（元/kWh），分析可再生能源的利用情况及蓄电池参与调节后产生的影响。

这一调度方案是在问题（3）的基础上允许弃风弃光，同理略作修改即可。

输出：

相比问题（3），本方案允许放弃高电价的新能源电力，因此可以进一步降低平均用电成本；相比问题（2），本方案多了蓄电池的调节作用（峰谷电价转移），因此也降低了平均用电成本，同时因为电池对新能源的消纳，本方案相对问题（2）也略微降低了弃风弃光率。

• input.csv

• microgrid_optimization.ipynb