最优化方法复习笔记（三）牛顿法及其收敛性分析

上一章传送门：

最近四项目并行多线程，还有悬空欲坠的数据结构课设=_=，所以嘛。。。更得会时快时慢啦。

最近在忙里偷闲学习manim，等有空，我会把几篇文章的插图换成manim制作的动画。（manim也就是3Blue1Brown制作视频的Python库）

牛顿法求解方程近似解
牛顿法在最优化上的应用
牛顿法与梯度下降法的比较
牛顿法的性质与收敛性分析

仿射不变性
局部收敛性
牛顿法搜索方向的下降性

牛顿法的优点与缺点
牛顿法的变种

阻尼牛顿法
混合方法
LM法

无论是否学过最优化，相信大家在初高中学习方程的近似解求解时，多多少少都接触过牛顿法。比如现在我们要求解 $f(x)=0$ 在 $\\mathbb R$ 上的解 $x^*$ ，就可以通过选取迭代初值 $x_0$ ，然后通过牛顿迭代公式迭代逼近 $x^*$ ：

$x_{t+1}=x_t-\\frac{f(x_t)}{f'(x_t)}\\\\$

这个方法也被称为Newton-Raphson方法

从几何角度切入，凭借感觉也能感觉这个方法能够收敛到 $x^*$ ：

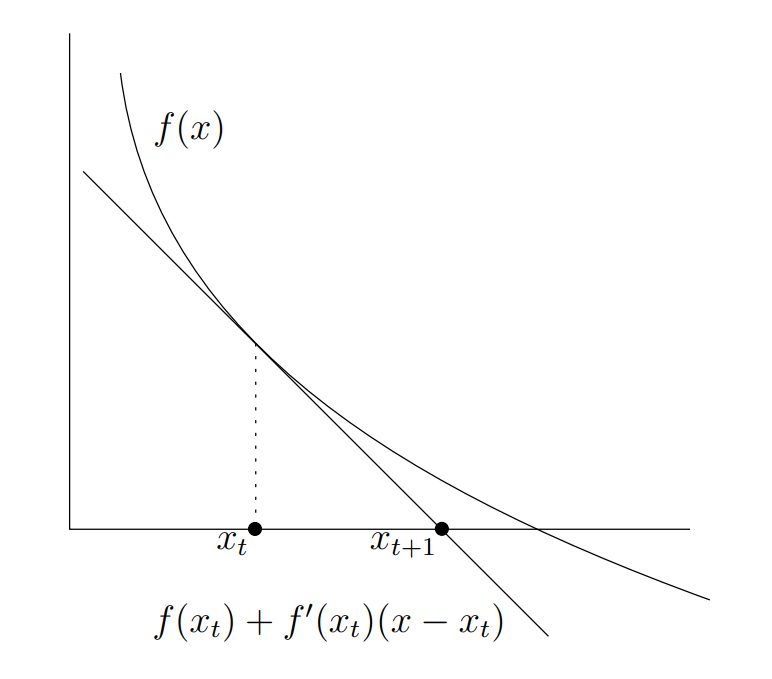
在 $x^*$ ?的小领域内，比如上述这幅图，可近似认为函数是单调的（比如单调递减），? $x_t$ 处的迭代理应将 $x_t$ ?向右移动。而由于函数是单调递减的，所以 $(x_t,f(x_t))$ ?处的切线的横截距确实相比较 $x_t$ ?而言更向右移动了，因此，将此横截距作为下一次的迭代点是符合我们的预期的。

当然，直观上的狡辩不能使人信服。我们可以尝试讲道理地说明一下牛顿法的合理性。将? $f(x)$ 在迭代初值 $x_0$ ?处Taylor展开可得：

$\\begin{align}f(x)=f(x_0)+f'(x_0)(x-x_0)+o(|x-x_0|) \\end{align}\\\\$ 舍去高阶项，可得：

$f(x)=f(x_0)+f'(x_0)(x-x_0)\\\\$ 将零点 $x^*$ ?代入其中可得：

$f(x^*)=0=f(x_0)+f'(x_0)(x^*-x_0)\\\\$ 因此可得：

$x^*=x_0-\\frac{f(x_0)}{f'(x_0)}\\\\$ 由于上式是舍去了高阶项后的近似，因此我们实际上并不能根据上式一步得到 $x^*$ ?。而要通过多步迭代，由此得到牛顿迭代方程：

$x_{t+1}=x_t-\\frac{f(x_t)}{f'(x_{t})}\\\\$

那为什么要在最优化的笔记上写上牛顿法呢？因为要用呀（废话）。

对于一阶可微的函数? $f:\\mathbb R\ o\\mathbb R$ ，根据费马定理，其极值点 $x^*$ ?满足? $f'(x^*)=0$ ，而最优化方法的目的也就是通过种种手段，求出或近似这个极值点? $x^*$ 。注意到牛顿法是用来求解函数 $g(x)$ ?的一个零点的近似值? $\\hat x$ 的，而最优化则是求解导数的零点的近似解，那么令 $g(x)=f'(x)$ ?，迭代出来的? $\\hat x$ 不就是极值点 $x^*$ ?的近似解了吗？

因此，使用牛顿法优化函数 $f$ 的迭代方程也就呼之欲出了：

$x_{t+1}=x_t-\\frac{g(x_t)}{g'(x_t)}=x_t-\\frac{f'(x_t)}{f''(x_t)}=x_t-f''(x_t)^{-1}f'(x_t)\\\\$

当然，这需要? $f$ 是二阶可导的，此处就默许我们研究的函数足够正则

上述为一维输入的情形，对于? $f:\\mathbb R^n\ o\\mathbb R$ 也有类似的迭代式：

$x_{t+1}=x_t-\ abla^2f(x_t)^{-1}\ abla f(x_t)\\quad\\quad x_t\\in\\mathbb R^n\\\\$ 其证明方法和一维情形几乎一致，由Taylor展开式：

$f(x_t+d)=f(x_t)+\ abla f(x_t)^Td+\\frac12 d^T\ abla^2f(x_t)d+o(||d||^2)\\\\$ 其中? $x_{t+1}=x_t+d$ ，? $d$ 为搜索方向。

舍去高阶项，并考虑搜索方向为变量的单值函数? $h(d)$ ：

$h(d)=f(x_t+d)=f(x_t)+\ abla f(x_t)^Td+\\frac12d^T\ abla^2f(x_t)d\\\\$ 为了使得单次迭代下降得尽可能多，我们需要最小化 $h(d)$ ?。所以，我们想要的方向? $d$ 为：

$\\begin{align}d&=\\arg\\min_{d}h(d)\\\\ \ abla h(d)&=\ abla f(x_t)+\ abla f^2(x_t)d=0\\\\ \\Rightarrow &\\boxed{d=-\ abla^2f(x_t)^{-1}\ abla f(x_t)}\\end{align}\\\\$ 因此，迭代方程为

$x_{t+1}=x_t+d=x_t-\ abla^2f(x_t)^{-1}\ abla f(x_t)\\\\$ 由是，我们得到了牛顿法优化函数的算法：

$\\begin{align}选定&迭代初值x_0\\in\\Omega,选取\\epsilon>0,重复以下操作:\\\\ &若||\ abla f(x_t)||<\\epsilon，停止循环\\\\ &计算梯度:\ abla f(x_t)\\\\ &计算Hessian矩阵:\ abla^2f(x_t)\\\\ &计算方向:d_t=-\ abla^2f(x_t)^{-1}\ abla f(x_t)\\\\ &更新迭代点:x_{t+1}=x_t-d\\\\ \\end{align}\\\\$

我们观察一下牛顿法：

$x_{t+1}=x_t-\ abla ^2f(x_t)^{-1}\ abla f(x_t)\\\\$ 有没有发现它和梯度下降法有点像？我们可以看一下固定步长的梯度下降法：

$x_{t+1}=x_t-\\gamma\ abla f(x_t)\\\\$ 可以发现，这两个方法都是基于当前迭代点的梯度信息进行搜索方向的选择的，只不过梯队下降法是在梯度的反方向上进行线搜得到下一个迭代点，而牛顿法则是通过Hessian矩阵在梯度上进行线性变换得到搜索方向（甚至步长都不需要确定）。所以牛顿法对函数在迭代点处的信息利用更加充分，直观来看，相比于梯度下降法，函数足够正则的情况下牛顿法迭代得更加准确，收敛速率也会更快。

比如还是拿正定二次型作为例子，无论使用哪种方式确定步长的梯度下降法，只要Hessian矩阵的条件数比较大，那么梯度下降法的迭代序列会依赖于迭代初值的选取，有的迭代初值会使得迭代序列抖动地靠近最优点，有的则只需要一步就迭代到了最优点。这一点我在上一篇文章中已经讨论过，实验结果如下：

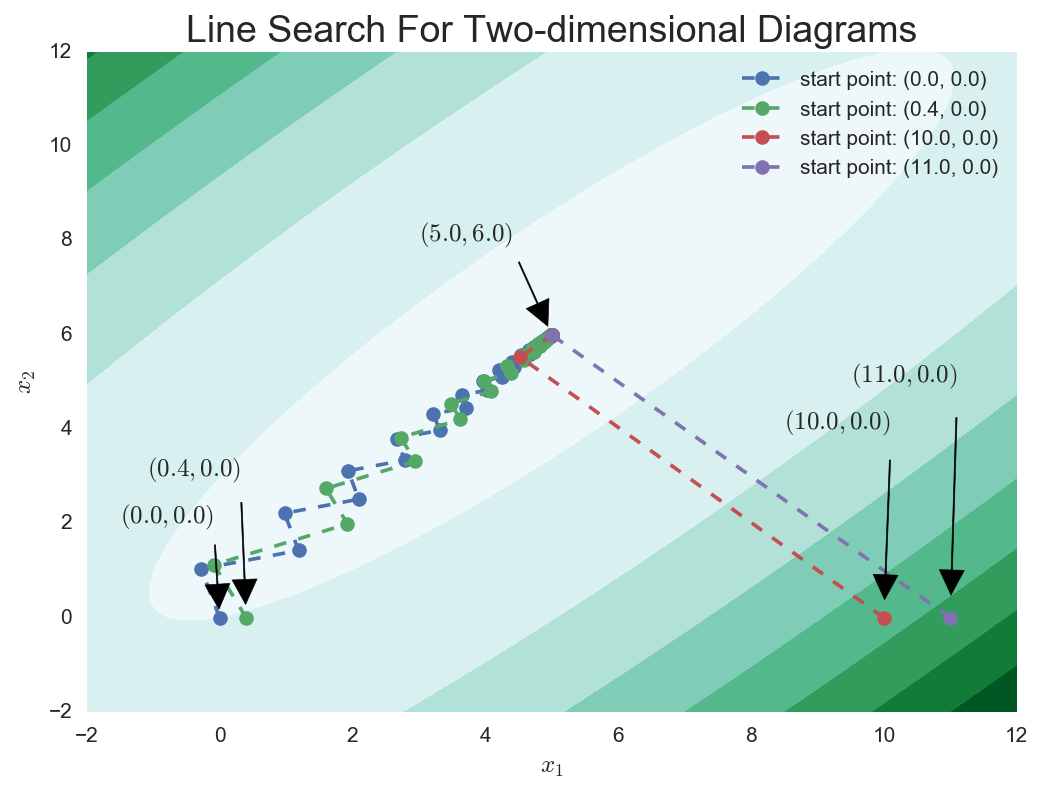
而对于牛顿法来说，无论迭代初值如何选取，它在正定二次形上的迭代只需要一步。

你可以做若干次实验来获取感性的认识。当然，不妨直接扔进牛顿法中看看能拿到什么有趣的结论：

我们之前研究的二次型为：? $f(x)=\\frac12x^TQx+b^Tx\\quad x\\in\\mathbb R^2$

令 $\ abla f(x)=0$ ?得到全局最优点? $x^*=-Q^{-1}b$ 。

下面实施牛顿法：

$\\begin{align}&选取迭代初值:x_0\\in\\mathbb R^2\\\\ &计算梯度:\ abla f(x_0)=Qx_0+b\\\\ &计算Hessian矩阵:\ abla ^2f(x_0)=Q\\\\ &计算方向:d_0=-\ abla^2f(x_0)^{-1}\ abla f(x_0)=-Q^{-1}(Qx_0+b)=-x_0-Q^{-1}b\\\\ &更新迭代式:x_1=x_0+d_0=-Q^{-1}b\\\\ &||\ abla f(x_1)||=0，停止循环 \\end{align}\\\\$

我们可以发现，只迭代一步，? $x_1$ 就恰好迭代到了全局最优点? $x^*$ ( $x_1=-Q^{-1}b=x^*$ ?)。因此，无论怎么选取迭代初值，二次型的Hessian矩阵的条件数有多么恶心，上述推导都保证了牛顿法可以帮我们一步迭代到最优点。

其实，我们可以从何另一个角度来解释为什么牛顿法迭代得如此之快。

所有基于梯度的迭代方程可以写成如下的形式：

$x_{t+1}=x_t-H(x_t)\ abla f(x_t)\\\\$

其中? $x\\in\\mathbb R^n,H(x_t)\\in\\mathbb R^{n\ imes n}$ 。

对于牛顿法来说，? $H(x_t)=\ abla^2f(x_t)^{-1}$

对于梯度下降法来说，? $H(x_t)=\\gamma I$

可以看到，牛顿法 $H$ 的?是随着当前迭代点的变化动态变化的，因此，相比于梯度下降法，牛顿法具有更加灵活的迭代过程。有的书上直接说牛顿法就是“自适应的梯度下降法”。

设 $f:\\mathbb R^n\ o \\mathbb R$ ?是二阶连续可微， $T:\\mathbb R^n\ o\\mathbb R^n$ ?是可逆仿射变换，记 $y=Tx$ ?，构造 $h(x)=f(Tx)$ ?，记单次迭代的牛顿步为? $n_x=-(\ abla^2 h(x))^{-1}\ abla h(x)$ ，则对于牛顿法单步迭代有：

$y+n_y=T(x+n_x)\\\\$ 这个式子说明：对于可逆仿射变换，牛顿法保持不变。

证明：

根据仿射变换的线性性，只需证明 $n_y=Tn_x$ 即可，也就是? $n_x=T^{-1}x_y$ ：

$\\begin{align}n_x&=-(\ abla^2 h(x))^{-1}\ abla h(x)\\\\ &=-\\Big( T^\ op\ abla^2f(y)T \\Big)^{-1}T^\ op\ abla f(y)\\\\ &=-T^{-1}\ abla^2f(y)\ abla f(y)\\\\ &=T^{-1}n_y \\end{align}\\\\$

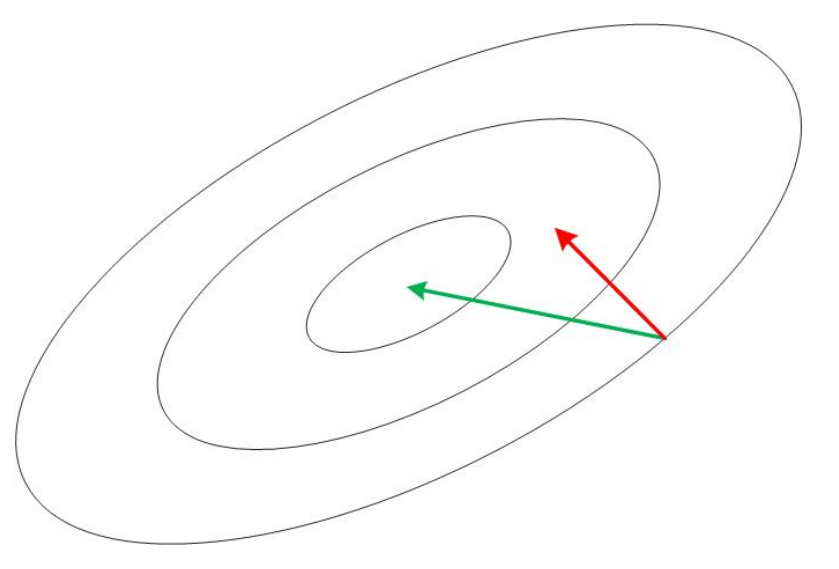
这个性质刻画了这么一件事：牛顿法确定的搜索方向会随着搜索空间的变换做出相应的变化。举个例子吧，如果我们的搜索空间是一块橡皮泥，我们把通过牛顿法得到的下降路线标出来（比如画出来），则如果我们将橡皮泥在我们的桌面上做一次仿射变换，那么得到的橡皮泥上的那些下降路线之间的相对位置是不变的。原来是三步到达最优点，也就是在原来的橡皮泥上是三条折线，仿射变换后的橡皮上的下降曲线还是三条折线。

用仿射不变性可以轻易解释为什么无论如何选取迭代初值，牛顿下降法都可以在任何的二次型上一步迭代到最优点：

对于Hessian矩阵条件数为1的二次型，牛顿法可以在任意迭代起点确定一条包含最优点的二次曲线，而最优点就在该曲线的最低点上。因此，对于条件数为1的二次型，牛顿法一步到位很显然。然后对于其他类型的二次型，都可以对条件数为1的二次型的搜索空间做仿射变换得到，而仿射变换下的牛顿法不变，因此，原来是1步到位，变换完后还是一步到位。

可以证明牛顿法在条件足够好的情况下，能够以极快的速度收敛到最优点（二次收敛）。毫不夸张地说，牛顿法是所有目前已知的迭代优化法中，收敛速率最快的了。

much faster than anything we have seen so far. . .

结论为牛顿法下，函数只需要最多? $\\log\\log\\frac{1}{\\epsilon}$ 步就能够使得得到的最优化近似解与实际最优点之间的距离小于 $\\epsilon$ ?。

但是，这些诱人的性质都需要迭代起点与最优点的距离足够近才能实现，别忘了当初推导牛顿法时，我们就舍弃了高阶项? $o(||d||^2)$ ，舍弃这一部分产生的误差在迭代跨度稍微大一点的时候是不好忽略的。

我们将以上的性质称为牛顿法的局部收敛性。

关于牛顿法的全局收敛性的结论也只是在2018年才被证明。

用一句话来概括上述的结论就是：牛顿法在靠近最优点处是二次收敛的。下面我们可以尝试证明这个结论。在证明这个结论之前，我们需要为“靠近最优点”定义一些合情合理的性质，从获得后续推导可能会用到的约束条件：

(1) Hessian矩阵的逆矩阵谱范数有界。也就是存在大于0的实数 $\\mu$ ?，使得：

$||\ abla^2f(x)^{-1}||\\le\\frac1\\mu,\\forall x\\in \ ext{dom}(f)\\\\$

这个性质被称为 bounded inverse Hessians ，可以证明确保目标函数满足该性质的一种方法是保证函数强凸。而此处的 $\\mu$ ?也恰为强凸系数。

(2) Hessian矩阵是Lipschitz连续的。也就是存在大于0的实数 $B$ ?，使得：

$||\ abla^2f(x)-\ abla^2f(y) ||\\le B||x-y||,\\forall x,y\\in\ ext{dom}(f)\\\\$ 接下来我们证明牛顿法靠近最优点时是二次收敛的：

我们记 $H(x)=\ abla^2f(x)$ ?，然后我们在牛顿迭代方程两边同时减去最优点? $x^*$ ：

$\\begin{align}x_{t+1}-x^*&=x_t-x^*-H(x_t)^{-1}\ abla f(x_t)\\\\ &=x_t-x^*+H(x_t)^{-1}(\ abla f(x^*)-\ abla f(x_t))\\quad\\quad(\ abla f(x^*)=0)\\\\ \\end{align}\\\\$ 设? $g(t)=\ abla f(x_t+t(x^*-x_t))$ ，则? $g'(t)=H(x_t+t(x^*-x_t))(x^*-x_t)$

根据微积分基本定理，我们有

$\\begin{align}\ abla f(x^*)-\ abla f(x_t)&=g(1)-g(0)\\\\ &=\\int_0^1g'(t)dt\\\\ &=\\int_0^1H(x_t+t(x^*-x_t))(x^*-x_t)dt \\end{align}$

故我们有

$\\begin{align}x_{t+1}-x^*&=x_t-x^*+H(x_t)^{-1}\\int_0^1H(x_t+t(x^*-x_t))(x^*-x_t)dt\\\\ &=H(x_t)^{-1}\\Bigg( H(x_t)(x_t-x^*)+\\int_0^1H(x_t+t(x^*-x_t))(x^*-x_t)dt \\Bigg)\\\\ &=H(x_t)^{-1}\\int_0^1(H(x_t+t(x^*-x_t))-H(x_t))(x^*-x_t)dt \\end{align}\\\\$

两边取范数，并由矩阵谱范数的定义（矩阵最大特征值）和积分不等式，可得：

$\\begin{align}||x_{t+1}-x^*||&=\\Bigg|\\Bigg| H(x_t)^{-1}\\int_0^1(H(x_t+t(x^*-x_t))-H(x_t))(x^*-x_t)dt\\Bigg|\\Bigg|\\\\ &\\le ||H(x_t)^{-1}||\\cdot\\Bigg|\\Bigg| \\int_0^1(H(x_t+t(x^*-x_t))-H(x_t))(x^*-x_t)dt\\Bigg|\\Bigg|\\\\ &\\le ||H(x_t)^{-1}||\\int_0^1||(H(x_t+t(x^*-x_t))-H(x_t))(x^*-x_t)||dt\\\\ &\\le ||H(x_t)^{-1}||\\int_0^1||(H(x_t+t(x^*-x_t))-H(x_t))||\\cdot||(x^*-x_t)||dt\\\\ &=||H(x_t)^{-1}||\\cdot ||x^*-x_t||\\int_0^1||(H(x_t+t(x^*-x_t))-H(x_t))||dt\\\\ \\end{align}\\\\$ 接下来，我们使用靠近最优点带来的“好处”，也就是上述定义的性质(1)和(2)。

由性质(1)可得， $\\exists \\mu>0$ ?，使得

$||H(x_t)^{-1}||\\le\\frac1\\mu\\\\$ 由性质(2)可得，? $\\exists B>0$ ，使得

$\\begin{align}\\int_0^1||H(x_t+t(x^*-x_t))-H(x_t) ||dt&\\le\\int_0^1 B||t(x^*-x_t)||dt\\\\ &=B||x^*-x_t||\\int_0^1tdt\\\\ &=\\frac B2||x^*-x_t|| \\end{align}\\\\$ 整合进原式可得：

$||x_{t+1}-x^*||\\le\\frac1\\mu||x^*-x_t||\\frac B2||x^*-x_t||=\\frac{B}{2\\mu}||x^*-x_t||^2\\\\$ 因此得到：

$\\frac{||x_{t+1}-x^*||}{||x_t-x^*||^2}\\le\\frac{B}{2\\mu}\\\\$

因此，牛顿法在靠近最优点处是二次收敛的。

关于牛顿法，说了这么多，但是我们一直没有严格证明过牛顿法单步迭代是否会下降。

这好吗？这不好。

实际上，我们能确定牛顿法方向在Hessian矩阵正定的函数上一定是一个下降方向。

想要证明牛顿方向是一个下降方向，也就是证明存在一个? $\\gamma_k>0$ 使得：

$f(x_k+\\gamma_k d_k)<f(x_k)\\\\$ 其中 $d_k$ ?是牛顿法确定的搜索方向? $d_k=-\ abla^2f(x_k)^{-1}\ abla f(x_k)$ 。

证明：

设 $g(\\gamma)=f(x_k+\\gamma d_k)$ ?，则? $g'(\\gamma)=\ abla f(x_k+\\gamma d_k)^Td_k$ ，因此? $g'(0)=\ abla f(x_k)^Td_k=-\ abla f(x_k)\ abla^2f(x_k)\ abla f(x_k)$

根据? $\ abla^2f(x_k)$ 的正定性，可得? $g'(0)<0$ 。

由导数的连续性可得 $\\exists \\gamma_k>0$ ?使得 $g(\\gamma_k)<g(0)$ ?，即 $f(x_k+\\gamma_kd_k)<f(x_k)$ ?。

因此，在满足迭代点处Hessian矩阵正定的情况下，我们能保证由牛顿法得到的方向是一个下降方向。

经过上面的一番论述，我们可以发现牛顿法的收敛速率等结果在数值上有很好看的、令人眼前一亮的结果。总结一下，牛顿法有如下的优点：

在最优点附近二次收敛，一般情形下收敛得也很快。
牛顿法具有仿射不变性，所以对坐标系的选择不敏感。
牛顿法不会随着问题维度的增大而大幅增加所需的迭代次数。
不需要通过线搜确定迭代更新的步长。

然而，在监督学习中，我们几乎不会使用牛顿法来优化损失函数，继而更新我们的模型参数，因为牛顿法有如下的几个缺点，优点很诱人，但是缺点同等致命：

计算和储存Hessian矩阵及其逆矩阵需要很高的成本。

每次迭代都需要计算Hessian矩阵，计算Hessian矩阵的代价是计算? $\\frac{n(n+1)}{2}$ 个偏导数；继而计算Hessian矩阵的逆矩阵，计算机一般是通过求解线性方程组来求解逆矩阵的，其时间复杂度为 $\\mathcal O(n^3)$ ?。因此，设计高效的自动二阶微分系统很困难。
如今能够计算和存储高精度的一阶导数信息已经是很不错的了，目前开源社区中我所熟知的通用型深度学习框架中，没有任何一款能够计算损失函数关于模型参数的Hessian矩阵。因而求取二阶信息的难度可见一斑。

无法保证Hessian矩阵是可逆的，同时也不能保证矩阵是正定的。
牛顿法得到的搜索方向不一定是下降的。通过上述论证，只有迭代点处Hessian矩阵正定才能保证牛顿法得到搜素方向是下降的。

之前已经论证过了，牛顿方向的下降性是依赖于迭代点处Hessian矩阵的正定性的。若? $x_t$ 处? $\ abla^2f(x_t)$ 非正定，则由牛顿法确定的方向 $-\ abla^2f(x_t)\ abla f(x_t)$ ?不一定是下降的。而阻尼牛顿法就是为牛顿方向加一个线搜索，以保证搜索方向的下降性：

$x_{k+1}=x_k-\\alpha_k\ abla^2f(x_k)^{-1}\ abla f(x_k)\\\\$

我们可以结合牛顿法和梯度下降法的特点，若牛顿方向可行，则使用牛顿法进行迭代，若不行，则使用梯度下降法确定搜索方向。

具体搜索方向选取的逻辑可以是这样的：

$\\begin{align}&if\\ \ abla^2 f(x_k)正定,则\\quad d_k=-\ abla^2f(x_k)^{-1}\ abla f(x_k)\\\\ \\\\ &if\\ \ abla^2f(x_k)负定,则\\quad d_k=\ abla^2f(x_k)^{-1}\ abla f(x_k)\\\\ \\\\ &else\\ \\quad\\quad d_k=-\ abla f(x_k) \\end{align}\\\\$

牛顿法中 $\ abla^2f(x)$ ?可能是奇异、非正定等情况，为了解决这个情况，我们可以为Hessian矩阵加上一个 $vI$ ?来强行让Hessian矩阵变得正定：

$(\ abla^2f(x_k)+vI)d_k=-\ abla f(x_k)\\\\$

其中? $v\\in\\mathbb R^+,I$ 是单位矩阵。凭借特征值分解的知识，我们很容易知道只要 $v$ ?足够大，那么? $\ abla^2 f(x_k)+vI$ 就一定是正定的。

下一张写拟牛顿法，但是在此之前，我得先把思政课的PPT做完(｀?ω?′)

下一章传送门：

锦恢：最优化方法复习笔记（四）拟牛顿法与SR1,DFP,BFGS三种拟牛顿算法的推导与代码实现

2024-04-29

行业资讯