?最优化方法分为传统优化方法和启发式优化方法两大类。传统优化方法大多利用目标函数的梯度 (或导数)信息实现单可行解的惯序、确定性搜索；启发式优化方法以仿生算法为主，通过启发式搜索策略实现多可行解的并行、随机优化。启发式搜索算法不要求目标函数连续、可微等信息，具有较好的全局寻优能力。

?在众多启发式优化方法中，差分进化算法是一种基于群体差异的启发式随机搜索算法，该算法是R．Store和K．Price为求解Chebyshev多项式而提出的。差分进化算法具有原理简单、受控参数少、鲁棒性强等优点。

?差分进化算法来源于早期提出的遗传算法（Genetic Algorithm，GA）。而差分进化算法引入了利用当前群体中个体差异来构造变异个体的差分变异模式，是其独特的进化方式。

?总而言之，差分进化算法（DE）是一种多目标（连续变量）优化算法（MOEAs），用于求解多维空间中整体最优解。

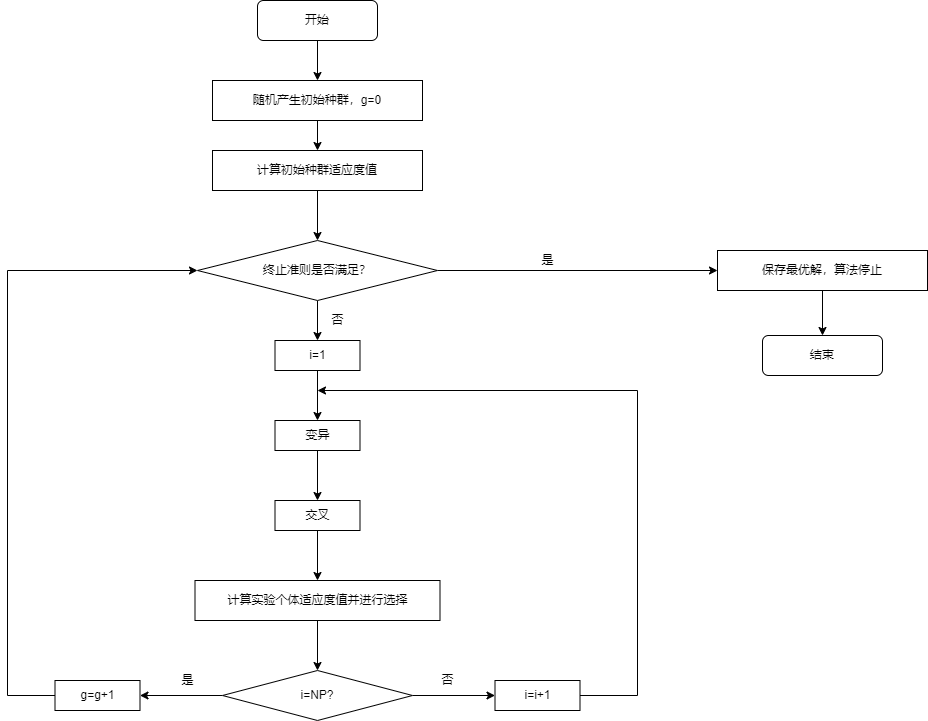
设解空间内存在NP个个体（即种群大小为NP），每个个体是D维向量。

初始种群随机产生：

表示第i个个体， 表示第j个分量， 表示第j个分量的下界， 表示第j个分量的上界。

差分进化算法使用种群中两个不同向量来干扰一个现有向量，进行差分操作，来实现变异。

第 代变异个体：

是从当前群体中随机选择的3个互不相同的个体，而且它们也不应与目标个体 相同。 为变异因子（缩放因子）， 为目标个体 对应的变异个体。

在进化过程中，为了保证解的有效性，必须判断变异个体中各分量是否满足边界条件，如果不满足边界条件，则变异个体用随机方法重新生成。

不同的差分策略，可以描述为DE/x/y/z。

其中参数 x 表示参与变异的向量，可以是随机向量 (rand)、当前种群的最优向量 (best) 或者是当前向量本身 (current)；

参数 y 表示参与变异的差分向量数目；

参数 z 表示交叉的模式，如二项式交叉、指数交叉以及正交交叉。

其中DE/ rand/ 1/ bin和DE/ best/ 2 /bin 是目前应用最为广泛的差分策略，其中第1种策略有利于保持种群多样性，第2种策略有利于提高算法的收敛速度。

对于每个个体和它所生成的子代变异向量进行交叉，具体的说就是对每一个分量按照一定的概率选择子代变异向量（否则就是原向量）来生成试验个体。

其中 为交叉概率因子， 为随机的一个分量，确保交叉后的试验个体至少有一维分量由变异个体提供。

差分进化算法使用贪婪算法，根据适应度函数的值，从目标个体和试验个体中选择更优的作为下一代。

通过以上的变异、交叉和选择操作，种群进化到下一代并反复循环，直到算法迭代次数达到预定最大次数，或种群最优解达到预定误差精度时算法结束。

DE 算法的控制参数主要有种群规模 NP、缩放因子 F 以及交叉概率 CR。

在经典 DE 算法中采用的是参数固定设置的方式，即参数在搜索之前预先设置好并且在整个迭代过程中保持不变。

种群规模(NP)主要影响种群的多样性以及收敛速度。它的取值范围一般在[5D，10D]之间（D为每个个体的维度）。

增大NP 可以提高种群的多样性，使得DE 算法更能收敛于最优解，但是会增加算法运行的时间复杂度。

减小NP 可以提高收敛速度，但易陷入局部最优，即早熟收敛。

当NP＜20 时，还容易发生停滞现象，停滞现象发生后算法不能收敛和继续向最优解方向搜索寻优，但种群继续保持着多样性以及非收敛状态。

变异因子(F)决定种群个体差分步长大小，影响算法最优解的搜索。它的取值范围一般在[0.4，0.95]之间。

增大F 可以加大算法的搜索空间，提高种群多样性，有利于算法搜索最优解，但会降低收敛速率。

减小F 可以增加算法的开发能力，提高算法的收敛速度，但同时增加陷入早熟收敛的风险。

交叉概率因子(CR)起着平衡算法全局与局部搜索能力的作用。它的取值范围一般在[0.3, 0.9]之间。

增大CR 可以提高种群多样性，但可能会造成算法后期收敛速度变慢。

减小CR 有利于分析个体各维可分离问题。

差分进化算法 (DE) 是进化算法簇中一个非常重要的新兴分支，在很多基准测试和实际应用问题上都表现出了卓越的性能，其新颖的差分进化操作起到了决定性的作用。

近年来针对 DE 算法的理论研究主要集中在如何提高算法的寻优能力、收敛速度以及克服启发式算法常见的早熟收敛以及搜索停滞等缺陷方面。 而改进差分进化算法可以朝着控制参数设置、差分策略选择、种群结构以及与其他最优化算法混合四大方向前进。