最近在整理和学习深度学习中的各种优化算法,在看 NAdam 的时候有一个疑问,一直没想明白。
我们知道 Nesterov 的公式形如
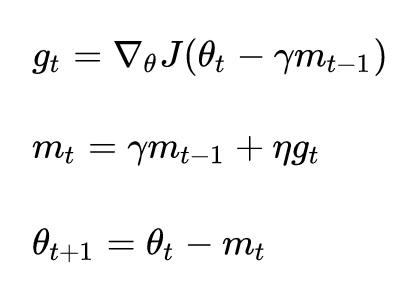
其中核心在于计算梯度的公式中,考虑到了「未来时刻」\ heta 的位置。
而我们知道 NAdam 就是把 Nesterov 思想加入了 Adam 中,但是 NAdam 却是先对 Nestrov 中的公式做了一个“等价变形”:
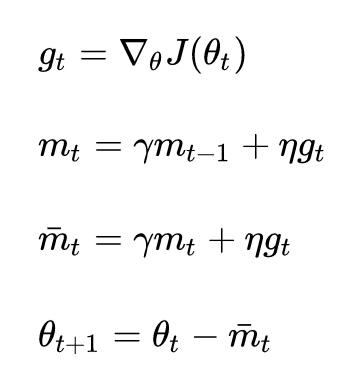
然后再用变形后的思路改写 Adam 的公式

自己花了好久才理解了这种改写的“等价性”。我疑惑的点在于,为什么要进行如此不直观的变形(原文:at the cost of some intuitive readability),而不是直接像 Nesterov 那样,直接改写求梯度公式为
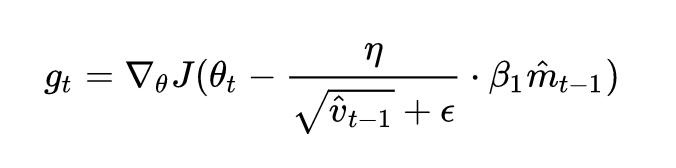
呢?
个人理解,这两种方式在理论上达到的效果是非常类似的,而原因作者在原文中只提了一句「we rewrite the NAG algorithm to be more straightforward and efficient to implement」。可能是我太菜了,一是没感觉出 straightforward,另一个是 efficient 上我对比两个公式感觉好像最多只是少了一次 element-wise multiply。
所以希望知道的是,这种理解是正确的么?除了少了一次运算之外,还有什么其他的理由让 NAdam 做了这种变形么?
Ref:
NAdam 的 paper: http://cs229.stanford.edu/proj2015/054_report.pdf
另外问题里不能写公式太难受了,上边提到的自己在整理的优化算法总结在 从 SGD 到 Adam —— 深度学习优化算法概览(一),NAdam 部分写了自己的理解。公式截图都是在那里截的,里面还有不少文字说明,FYI。
找到论文,给里面的通讯作者发邮件。
之所以这样等价变换,是因为在深度学习的代码实现层面上,第二种要比第一种省事啊。因为几乎所有深度学习框架,用的是自动求导,你没办法直接用梯度的解析式的
随手推了一下,如图。
至于为什么要这么变换,论文里说了"to be more straightforward and efficient to implement",其实就是这样变换公式看起来更简洁、形式上更直观,更直白的说,就是下面写论文的时候,用这个式子好写一点。
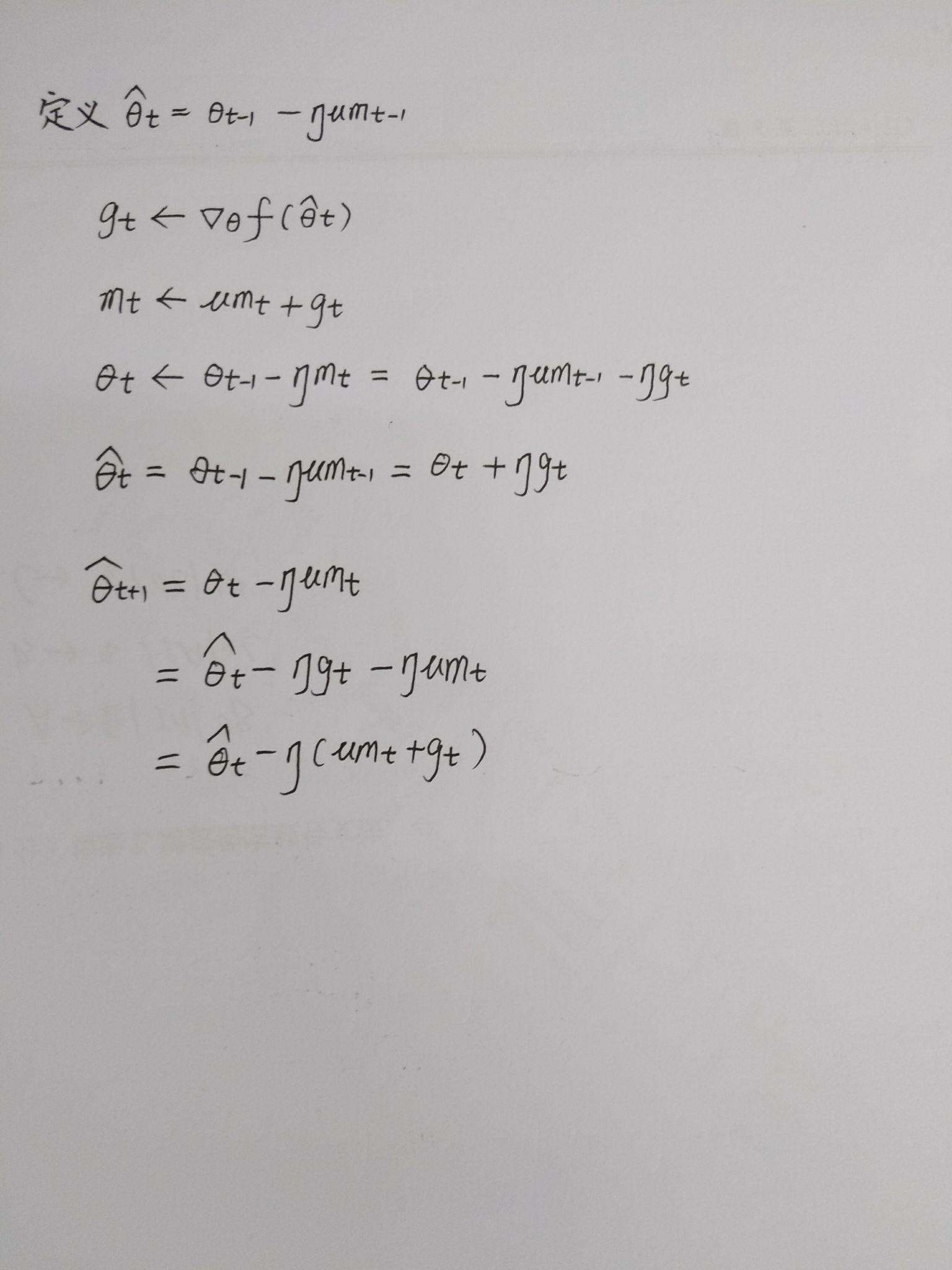
先说结论。个人认为NAdam和Nesterov+Adam没有本质上的区别。结论的得出主要参考自一下两篇文章:
Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747.
Dozat, T. (2016). Incorporating nesterov momentum into adam.
在介绍NAdam之前,我们梳理一下Adam的算法形成过程。
Adam算法是传统的momentum和RMSProp的结合。
基本的梯度下降方法:利用算法一的更新规则。

传统的momentum算法:积累之前的动量来替代原本的梯度,解决SGD的摇摆问题。
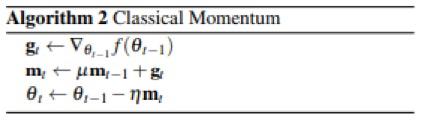
基于L2正则项的方法:具有自适应学习率的方法。
a. AdaGrad算法:其对于低频特征的参数选择更大的更新量,对于高频特征的参数选择更小的更新量。
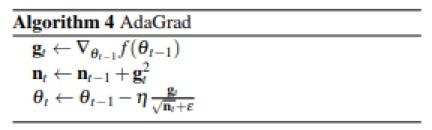
b. RMSProp算法:对AdaGrad的改进

将传统的momentum和RMSProp结合,便得到了Adam算法:

为什么要介绍Adam的形成过程呢?是因为NAdam其实和他的形成过程类似。
NAdam是 Nesterov accelerated gradient (NAG)和Adam的结合。我们先分别看看两者是什么:
Nesterov accelerated gradient (NAG):是一种 Momentum 算法的变种,其核心思想会利用 “下一步的梯度” 确定 “这一步的梯度”,当然这里 “下一步的梯度” 并非真正的下一步的梯度,而是指仅根据动量项更新后位置的梯度。
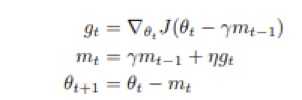
在上述的公式中,mt-1被应用了两次:一次是计算梯度gt,一次是计算θt+1。
然后我们应用一个look-ahead momentum vector来重新表示以上过程。值得注意的是,这个表示仅仅是为了计算的简洁性,并没有提出猜想的别的意思喔。和传统动量算法
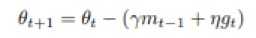
相比较可以看出,其实质就是把mt-1换成了look ahead mt。
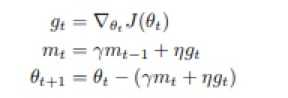
接下来,我们将Nesterov momentum加入到Adam当中,即利用当前的Nesterov动量向量来代替Adam中的传统动量向量。
首先,Adam算法的更新规则如下,注意,此处的vt,是Algorithm 6中的nt,β1是Algorithm6中的μ,并且在结合Nesterov和Adam的过程中,不需要修改nt
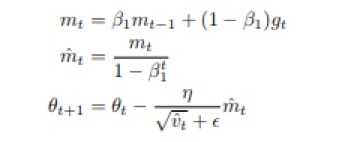
将上式展开可得:
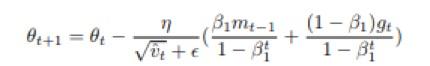
因为:
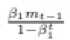
仅仅是动量向量的偏差修正项,因为上式可以转化为:
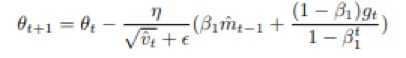
这个方程看起来非常类似于传统的动量算法的展开项
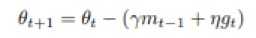
。我们现在可以同之前的操作一样添加Nesterov动量,用当前动量向量的偏置校正估计
替换上一时间的偏置校正估计mt-1,就得到了Nadam的更新规则:
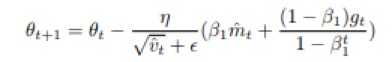
梳理了一遍NAdam的形成过程之后,我们发现其实这个算法主要就是将Nesterov动量来替换原来的Adam中的传统动量,中间形式的转化只是为了计算和表示的简洁性。毕竟NAdam更重要的是方法思想上的结合,中间的这个转化操作其实无伤大雅,不会对他们造成本质上的区别了。
?
本文来自公众号“AI大道理”
训练一个神经网络,我们想要得到误差最小,就是要我们的损失函数最小。
如何得到最小值呢?
这就是优化算法。
梯度下降法是众多优化中的一种。
1、损失函数
2、GD(梯度下降法)
3、BGD(批量梯度下降法)
4、SGD(随机梯度下降法)
5、MBGD(小批量梯度下降法)
6、小总结
7、牛顿法
8、Momentum(动量梯度下降法)
9、nesterov
10、AdaGrad(自适应梯度下降法)
11、AdaDelta
12、RMSProp
13、Adam
14、Nadam
15、为什么还是SGD用的多?
16、大总结

?
1、损失函数
梯度下降法是对一个函数进行求解最小值的方法。
先让我们看一看损失函数是什么?
Loss Function 是定义在单个样本上的,算的是一个样本的误差。
Cost Function 是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
以交叉熵损失函数为例:
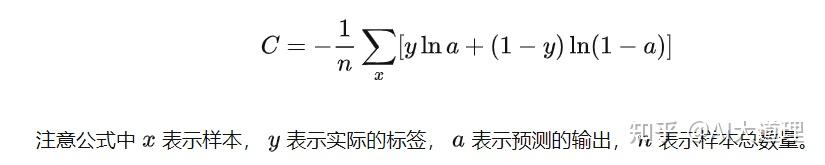
?
我们要最小化这个损失函数。
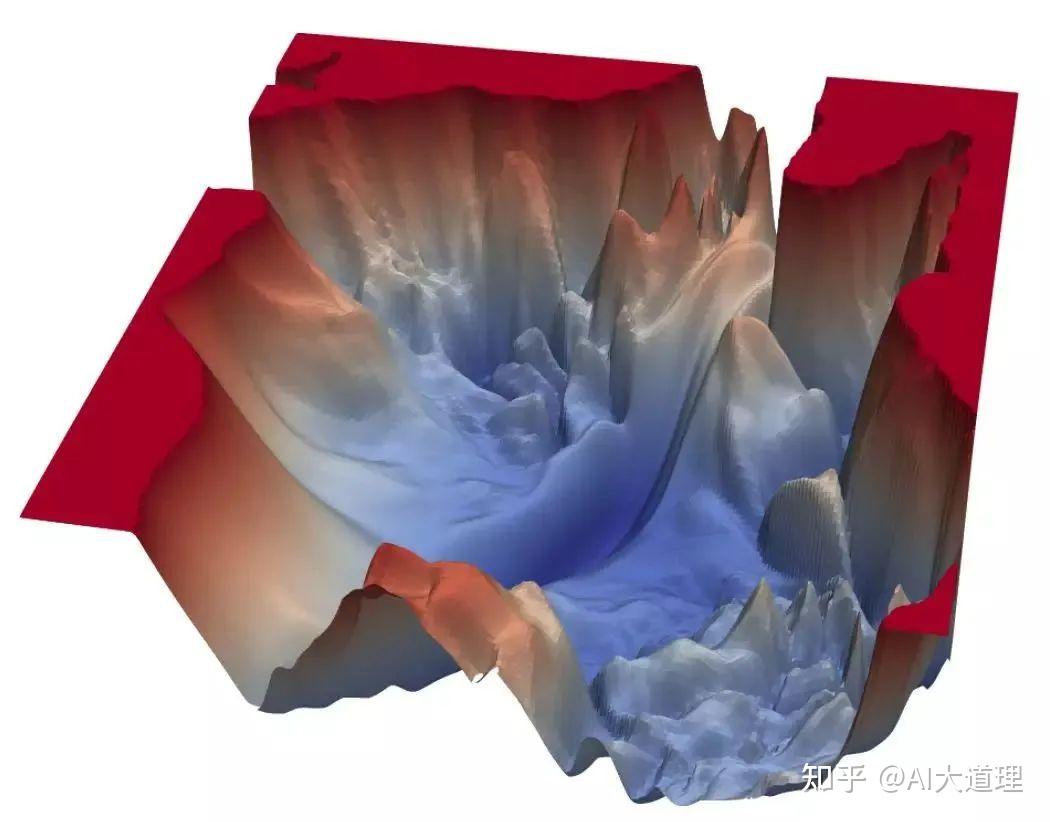
然而非凸的目标函数往往起起伏伏,拥有无数个高地和洼地。
?
模型进行训练时使用梯度下降,求得的是局部最小值而不是全局最小值,因为损失函数一般是非凸的。
至于为什么损失函数是非凸的,依据凸函数的性质,二阶导非负。所以要证明非凸,找个反例就好了。
事实上,凸优化问题是优化问题中的一种特例,是一种多种限制条件下才得到的简单问题。而现实中显然没有那么巧能被限制成一个凸优化问题。

?
2、GD(梯度下降法)
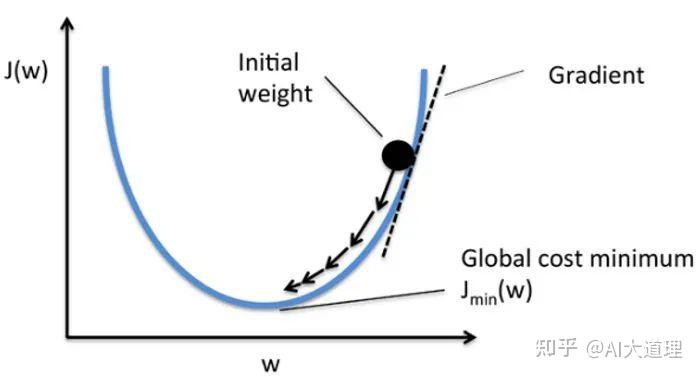
GD:gradient descent,梯度下降法是反向传播的一种算法,也是最常用的算法。
梯度下降法,沿着梯度负方向前进。
?
为什么是负方向?
梯度的方向是正方向,就是越来越大了,而负方向才是越来越小。
下降的多少由学习率a决定。
参数的更新方式:
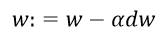
?

?

?
3、BGD(批量梯度下降法)
BGD:batch gradient descent。
GD梯度下降法是一个共同的概念,是最原始的算法。
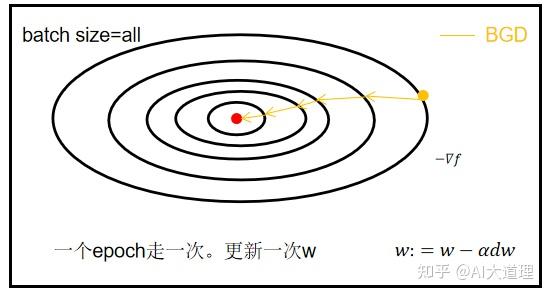
BGD是将梯度下降法用到神经网络中,是优化算法在神经网络中最原始的算法。
BGD需要全部训练样本参与计算,保证算法精准度,找到全局最优解。
BGD一个epoch更新一次参数。

?
?
优点:
1、全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。
2、BGD可以收敛于最优解,凸函数中为全局最优解,非凸中为局部最优解。
缺点:
1、计算全部训练样本更新梯度需要很多的内存开销。
2、更新慢,优化速度慢。
总之BGD的缺点就是优化慢,数据多。
慢,是否有更快的路径?
多,能否少部分训练?

?
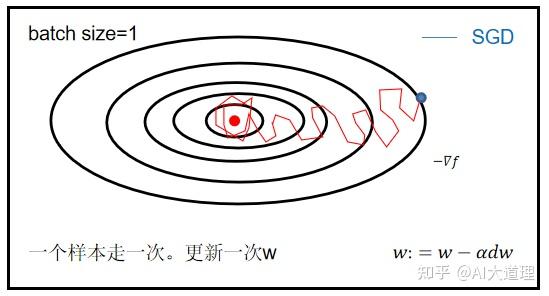
4、SGD(随机梯度下降法)
SGD:Stochastic Gradient Descent。
SGD是为了避免BGD在样本数量大时带来的巨大计算量。
SGD每次更新只选择一个样本。
即随机调一个数据计算,一个样本更新一次参数。

?
?
优点:
1、由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
1、SGD牺牲了一点精准度,单个样本并不能代表全体样本的趋势。
2、SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。但是大体上是往着最优值方向移动。
3、不收敛,在最小值附近波动。SGD会在最优点附件震荡,达不到最优解。

?
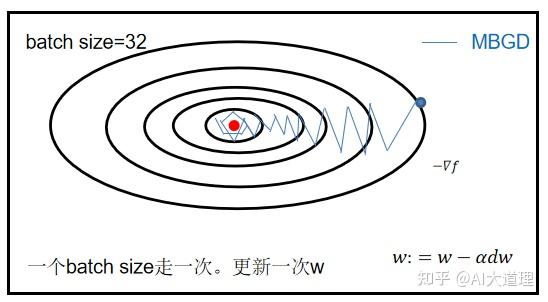
5、MBGD(小批量梯度下降法)
MBGD:Mini-batch Gradient Descent。
SGD选择的是一个样本更新一次,太少,不及;
BGD选择一整个样本更新一次,太多,过。
MBGD选择将样本划分为多个小块,将每个小块看作是一个样本,这样即保证了对数据模型的精准刻画,也不会太慢,中庸。
对于深度学习而言,所说的随机梯度下降SGD,其实就是基于小批量(mini-batch)的随机梯度下降。
SGD相当于batch size=1,BGD相当于batch size=all,MBGD相当于batch size=8,16,32等。

?
?
优点:
1、MBGD速度比BGD快,精度比SGD高。
2、在路径上,结合了SGD和BGD,达到一个相对中庸的路线。
3、BGD虽然也到达不了最优点,但是比SGD更接近最优点,在其附件震荡的幅度也较小。
缺点:
1、MBGD速度比SGD慢,精度比BGD低。
2、BGD到达不了最优点。
3、batch size的不当选择可能会带来一些问题。
batch size取多大?
1、batch size=1,退化为SGD,batch size=all,即BDG。
2、更大的批量会计算更精确的梯度,但是回报却是小于线性的。
3、极小的批量通常难以充分利用多核结构。当批量低于某个数值时,计算时间不会减少。
4、批量处理中的所有样本可以并行处理,内存消耗和批量大小会成正比。对于很多硬件设备,这是批量大小的限制因素。
5、在使用GPU时,通常使用2的幂数作为批量大小可以获得更少的运行时间。一般,2的幂数取值范围是32~256。16有时在尝试大模型时使用。
6、在一定范围内,一般来说 Batch_Size 越大,其确定的下降方向越准,引起训练震荡越小。

?
6、小总结
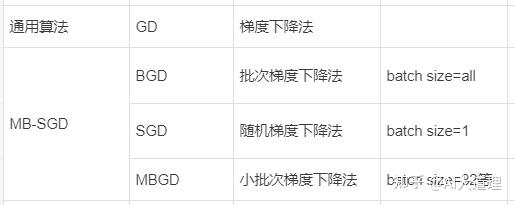
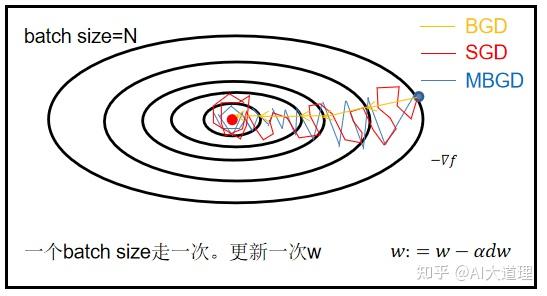
GD梯度下降法是通用的算法,将其用到深度学习中是MB-SGD。
在深度学习中讲SGD一般指的是MB-SGD。
BGD、SGD、MBGD只是MB-SGD的batch size取值不同而已。
?
?
灵魂的拷问1:
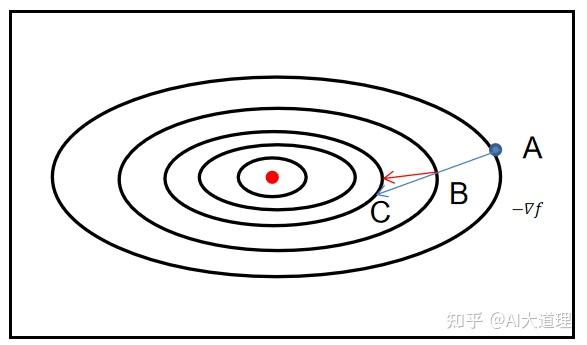
负梯度已经是下降最快的方向了,梯度下降法为什么还要优化路径?还能更快吗?
负梯度是下降最快的方向没错,但由于步长的存在,导致路径不是最优的。
只是朝着一开始最快的方向,一开始最快并不是一直最快。
A到达C是在A点沿着负梯度进行的,步长为AC,但在B点看,BC已经不是梯度下降最快的方向了。
?
为了一直沿着最快的方向下降,就要减少步长,减少步长就将减缓下降的速度,使得训练很慢。
灵魂的拷问2:
梯度下降法居然不是最速下降法?
梯度下降法不等于最速下降法。
最速下降法学习率不确定,是要搜索的,而梯度下降法学习率是确定的,是事先给出的。
梯度下降法是最速下降法使用欧式范数的特殊情况。

?
可见步长a是要求的,且是最小化函数值的a,然后再更新下一个。
求步长的作用就是在确定迭代方向的前提上,确定在该方向上使得函数值最小的迭代步长。
这样才是真正的最速下降。
对于梯度下降法,我们需要预先设定步长α。
而最速下降法的步长α是通过一个优化函数计算得到的。
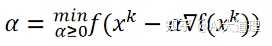
?
灵魂的拷问3:
神经网络是非凸的,为什么可以应用优化算法?
由于使用了非线性激活函数,模型的损失函数通常是非凸的。
应用优化算法只求得局部最优点,而没有求得全局最优点。
那么这样偏差大吗?
在高维中,局部最优点可能较接近全局最优点。
另外,在数据非全集中训练神经网络必然导致过拟合现象,且无法根治。
因此,仅求得局部最小点甚至带来一点正则化效果。
没有那么精确不一定是坏事。
引问:如何优化梯度下降法?
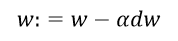
?
从w的更新公式看只有三个方向。
方向一、可使a学习率变化,即改变步长。
方向二、可使得dw改变,即改变方向。
方向三、w更新前对w处理,可使之变小,即权重衰减。

?
7、牛顿法
目标函数J(W)可以按泰勒展开,如果只取泰勒展开的二阶项,则J(W)可以近似表达为W的二次函数,即:
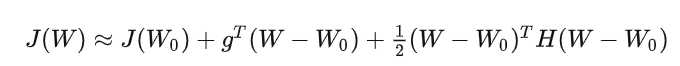
?
其中g为梯度向量,H为Hessian矩阵。
求导,并令导数可得。
牛顿方向:
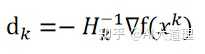
?
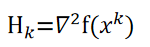
?
更新方式:
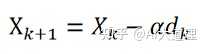
?
以上是高维的更新方式,一元函数的更新方式更加直观,即一阶导除于二阶导。
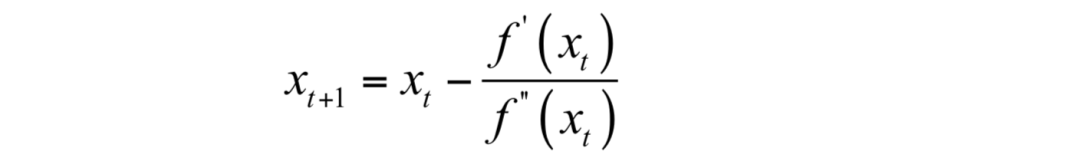
?

?
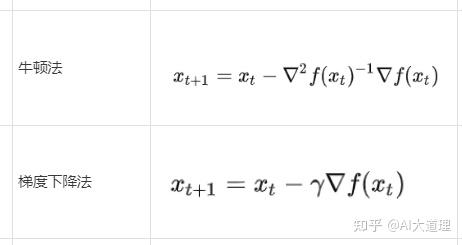
?
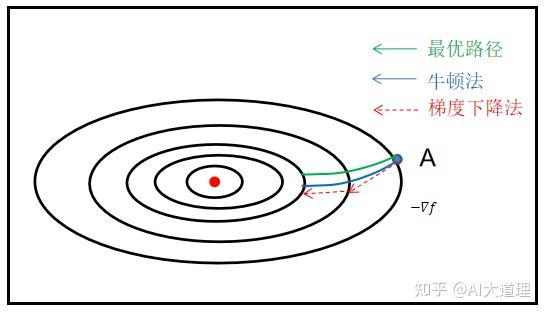
这两个方法都是基于当前迭代点的梯度信息进行搜索方向的选择的。
只不过梯队下降法是在梯度的反方向上进行线搜得到下一个迭代点,而牛顿法则是通过Hessian矩阵在梯度上进行线性变换得到搜索方向(甚至步长都不需要确定,或者说是1)
即两则的更新方向不一样。
?
优点:
1、对于二次正定函数,迭代一次即可以得到最优解,对于非二次函数,若函数二次性较强或迭代点已经进入最优点的较小邻域,则收敛速度也很快。
缺点:
1、计算量相当复杂,除需计算梯度除外,还需要计算二阶偏导数矩阵和它的逆矩阵,计算量,存储量都很大。
2、当海森矩阵非正定时牛顿法会失效。
3、保证不了迭代方向是下降方向,这就是致命。
致命问题的解决就是拟牛顿法。
拟牛顿法:
拟牛顿法的思想是不计算目标函数的Hessian矩阵然后求逆矩阵,而是通过其他手段得到Hessian矩阵或其逆矩阵的近似矩阵。
具体做法是构造一个近似Hessian矩阵或其逆矩阵的正定对称矩阵,用该矩阵进行牛顿法的迭代。
二阶方法能求得更高精度的解,而在深度神经网络中对参数的精度要求不高,不高精度的模型能提高泛化能力。另外二阶方法计算量太大,并不适用。
既然没必要,那就在一阶方法里面优化吧。

?
8、Momentum(动量梯度下降法)
SGD with momentum。
momentum,模拟动量,充分考虑前一阶段下降的惯性,像滚下山一样。
SGD的问题是,更新方向完全依赖于当前的样本,梯度方向也完全依赖当前样本及其得到的误差,因此更新不稳定。
引入momentum动量v,就是在对当前样本进行梯度更新时,同时考虑历史的更新方向。
v就是指数平均的作用,将过去的更新方向和当前的梯度方向进行加权。
直观点,就是原始SGD在梯度方向上直接做下降,现在把历史的梯度信息也考虑进来,因此优化时会有两个矢量相加的效果。下降方向变成了两个矢量方向的中间方向。
一阶动量是各个时刻梯度方向的指数移动平均值,约等于最近 1/(1?β1) 个时刻的梯度向量和的平均值。
一阶动量(梯度的移动加权平均)是在方向上相互抵消来防止震荡(震荡即走弯路),因为一阶是一个向量有不同方向。
也就是说,t时刻的下降方向,不仅由当前点的梯度方向决定,而且由此前累积的下降方向决定。
这就是惯性。
一阶动量:
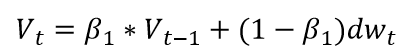
?
参数更新:
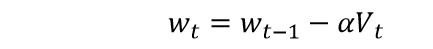
?
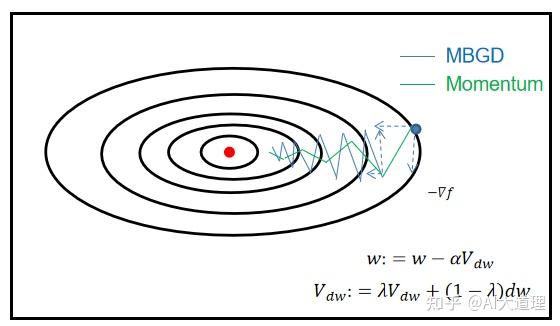
?
震荡来源于y方向,可利用历史数据,修正当前分量。
y轴和历史的相加,方向相反,所以y轴的量就变少了,而x轴由于方向一致,所以x轴的量变大了。
这个历史数据应该越近的数据权重越大。
当然,动量梯度下降法是考虑了所有历史数据,只是分派了不同的权重。

?
越远的地方权重指数减少,对历史数据都有加权。
优点:
1、动量移动得更快。
2、减少了震荡的幅度。
3、动量有机会逃脱局部极小值(因为动量可能推动它脱离局部极小值)。

?
9、nesterov
momentum是参考历史数据,nesterov还可以参考未来的数据。
超前一步,回马枪。
由于momentum考虑了历史的梯度信息,可以加速优化的进程,但如果参数已经处于最优附近,很有可能会因为累积的梯度导致过大的动量,再一次远离最优。
因此Nesterov期望参数在快到最优解时,适当调整当前的优化距离。
我们知道在时刻t的主要下降方向是由累积动量决定的,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果跟着累积动量走了一步,那个时候再怎么走。
因此,nesterov不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向。
更新方式:
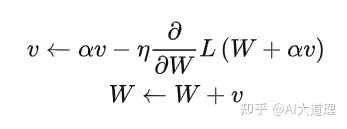
?
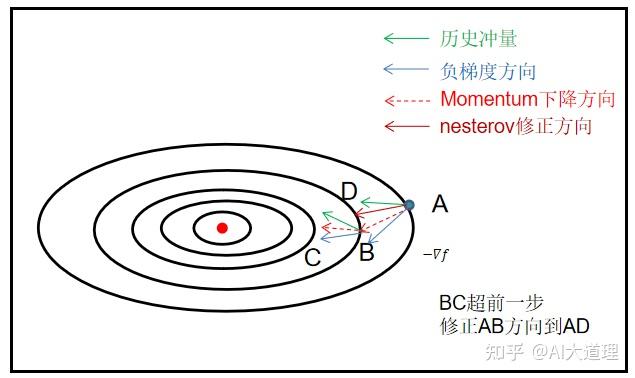
?

?
10、AdaGrad(自适应梯度下降法)
AdaGrad算法,即adaptive gradient,自适应梯度法。
AdaGrad通过记录每次迭代过程中的前进方向和距离,从而使得针对不同问题,有一套自适应调整学习率的方法,即不同的参数是需要不同的学习率的。
AdaGrad使得具有损失较大偏导的参数相应地有一个快速下降的学习率,而具有小偏导的参数在学习率上有相对较小的下降。
说人话:动态调节学习率的算法,经常更新的参数,学习率就小一些,不常更新的学习率就大一些。
AdaGrad,不是像动量一样跟踪梯度之和,而是跟踪梯度平方之和,并使用这种方法在不同的方向上调整梯度。
二阶动量,即以往所有梯度的平方和。
二阶动量:
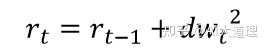
?
参数更新:
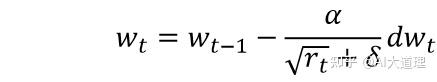
?

?
学习率除一个数值,这个数值是历史上所有梯度数据的平方再开方。
dw^2越大,学习率越小,使得学习率自适应。
假设一个参数累计历史梯度极大,那么经过计算更新这一步之后,他的学习率反而会变小。
相反的,如果一个参数累计历史梯度极小,那么经过计算更新这一步之后,他的学习率反而会变大。
累加的太快,学习率小的太快,导致最后学习很慢。
优点:
1、靠历史数据使得学习率自适应的。
缺点:
1、频繁更新的学习率可能过小,甚至消失。
2、对于训练深度神经网络模型而言,从训练开始时累积平方梯度值会越来越大,会导致学习率过早和过量的减少,从而导致迭代后期收敛及其缓慢。
3、需要手动设置全局学习率。
4、AdaGrad 非常慢。
5、梯度的平方和只会增加而不会减小
频繁更新的学习率可能过小,甚至消失怎么办?
问题解决:RMSProp

?
11、AdaDelta
Adadelta和RMSprop都是针对Adagrad学习速率衰减过快问题作出的改进。
改进思路和RMSprop很像,但是其背后是基于一次梯度近似代替二次梯度的思想。
Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是近似计算对应的平均值。
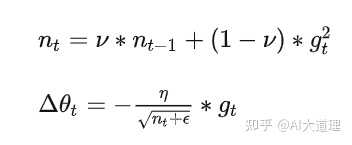
?
经过近似牛顿迭代法之后:
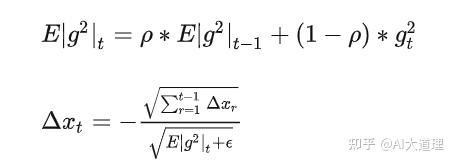
?

?
12、RMSProp
RMSProp:root means square prop
RMSProp 主要是为了解决 AdaGrad 方法中学习率过度衰减的问题。
AdaGrad 根据平方梯度的整个历史来收缩学习率,可能使得学习率在达到局部最小值之前就变得太小而难以继续训练;
RMSprop可以算作Adadelta的一个特例:
RMSProp 使用指数衰减平均(递归定义)以丢弃遥远的历史,使其能够在找到某个“凸”结构后快速收敛;此外,RMSProp 还加入了一个超参数 β2 用于控制衰减速率。
RMSProp主要思想:使用指数加权移动平均的方法计算累积梯度,以丢弃遥远的梯度历史信息(让距离当前越远的梯度的缩减学习率的权重越小)。
衰减率表明的是只是最近的梯度平方有意义,而很久以前的梯度基本上会被遗忘。
二阶动量:
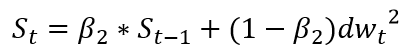
?
参数更新:
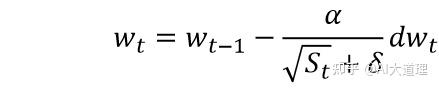
?

?
一阶动量将dwt变为vt,这里为什么不呢?
于是就有了Adam。

?
13、Adam
Adam:Adaptive Moment Estimation
融合了AdaGrad和RMSProp的Adam算法。
Adam算法的本质:其实就是Momentum+RMSProp的结合,然后再修正其偏差。Adam对梯度的一阶和二阶都进行了估计与偏差修正,使用梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率(参数更新的幅度)。
一阶动量:
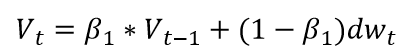
?
二阶动量:
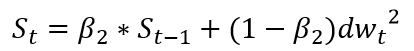
?
参数更新:
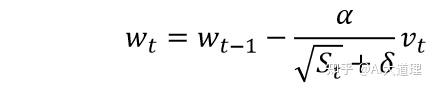
?

?
Nesterov能超前一步修正当前方向,Adam为什么不呢?
于是有了Nadam。

?
14、Nadam
Nadam类似于带有Nesterov动量项的Adam。

?
Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。

?
15、为什么还是SGD用的多?
从最初的SGD算法到Nadam算法,优化一直在进行,看起来算法越来越好了。
一般对于算法得优化,如果越来越好,使用的也就越来越多了。
然后深度学习优化算法是个异类。
优化了半天,现实中还是SGD用的最多,为什么?
1、自适应学习率方向的优化
就学习率来说,采用某个方式使得学习率随着时间变化只是一种偷懒行为,或者说是一种傻瓜式的操作。
这种操作并不代表这样的学习率就是最好的,最有效果的。
我们知道学习率一开始要大些,快速下降,后面要小些,慢慢收敛。
这是学习率的大致改变方向。
至于这个方向下如何改变才是最好的还是一个未知数。
因此基于学习率自适应的优化对整体性能的提升起到多少实质性的作用还是一个未知数,只知道方便了,我不用管学习率了。
而方便的同时也失去了对它更得心应手的控制力。
2、精确度方向的优化
一方面,在找不到全局最小值情况下,局部最小值精确一点或者不精确一点,大差不差。
另一方面,就模型的泛化能力和最终精确度而言,我本不想那么精确,因为训练的越精确可能过拟合就越严重。从这一点出发,不仅可以接受不能找到全局最小值只能找到局部最小值这一点,也可以接受局部最小值附件的点,甚至更差的点。(主,不在乎)
因为我们完全不知道哪个值才是最中庸的值,只知道不能太差,同时也不能太过精确了。
所以,从大局上考虑,精确度方向的优化似乎没有这个必要,是一个可有可无的优化。
3、随着GPU硬件性能的提升,速度上的差异不大。
使用Adam方便,快;使用SGD更灵活,也没有慢很多。
因此,各大算法孰优孰劣并无定论,SGD依然屹立不倒,甚至用的最多。
这也导致各种优化算法都有人用,以至于用哪个算法不是基于算法本身的好坏,而是基于你对这个算法的熟悉程度和喜好。
(以上只是梯度下降法系列的选择,牛顿法还是要果断pass的。)

?
16、大总结
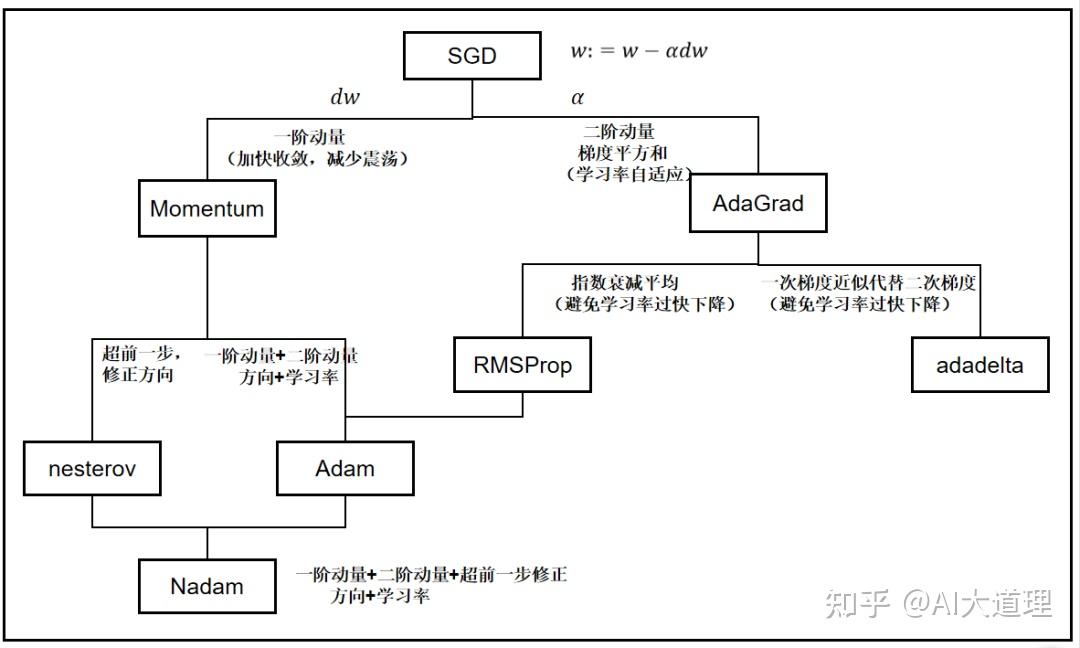
基于从山上滚小球的原理,在基础的梯度下降中增加了动量项得到了Momentum。
然后基于不是盲目选择下坡,而是要在遇到倾斜向上时减慢速度的原来,在Momentum增加了计算下一次参数所在位置,得到了nesterov。
考虑到传统梯度下降算法学习率一直不变造成了很多问题,因此通过增加梯度平方积累量,以达到学习速率自适应,从而得到了Adagrad。
由于学习速率减小过快会导致提前终止,为了解决这一问题又产生了Adadelta和RMSprop。
结合了Momentum和RMSprop的算法就是Adam。
融合了nesterov和Adam算法就是Nadam。
?
——————
浅谈则止,细致入微AI大道理
扫描下方“AI大道理”,选择“关注”公众号
—————————————————————
—————————————————————
|
留言吧?




 首页-富联娱乐-富联中国加盟站
首页-富联娱乐-富联中国加盟站
