网上关于Adam优化器的讲解有很多，但总是卡在某些部分，在此，我将部分难点解释进行了汇总。理解有误的地方还请指出。

Adam，名字来自：Adaptive Moment Estimation，自适应矩估计。是2014年提出的一种万金油式的优化器，使用起来非常方便，梯度下降速度快，但是容易在最优值附近震荡。竞赛中性能会略逊于SGD，毕竟最简单的才是最有效的。但是超强的易用性使得Adam被广泛使用。

Adam的推导公式：

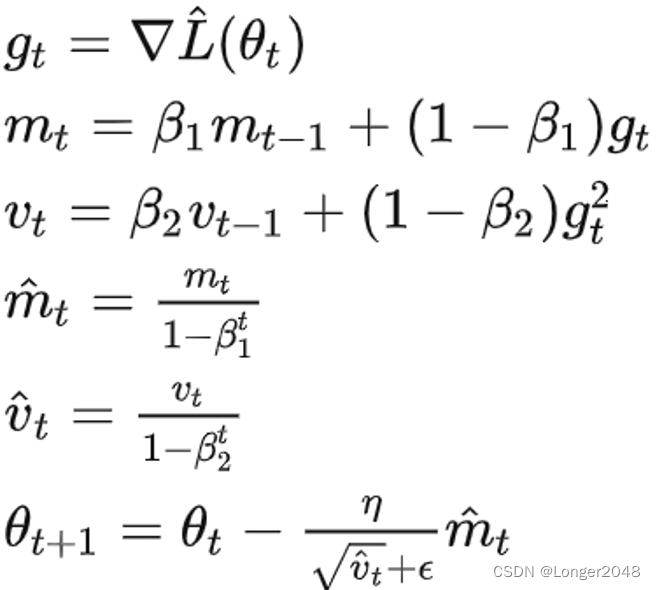
解释：

第一项梯度g_{t}就是损失函数\hat{L}对 heta_{t}求偏导。

第二项m_{t}为t时刻，梯度在动量形式下的一阶矩估计。

第三项v_{t}为梯度在动量形式下的二阶矩估计。

第四项\hat{m_{t}}为偏差纠正后的一阶矩估计。其中：\beta_{1}^{t}是贝塔1的t次方，下面同理。

第五项\hat{v_{t}}为偏差纠正后的二阶矩估计。

最后一项是更新公式，可以参考RMSProp以及之前的算法。

问题：

1. 梯度下降：不懂梯度下降建议先搞懂SGD优化器。

2. 动量：在之前的SGDM优化器中就被应用了。

3. 矩估计：不懂请看大学里面的《概率论与数理统计》。

4. 为什么需要偏差纠正：

这里只是讲讲我的理解。拿二阶矩估计v_{t}来举例，各个v_{t}的公式如下：

\begin{align*} v_{1}&=(1-\beta_{2})g_{1}^2\\ v_{2}&=\beta_{2}v_{1}+(1-\beta_{2})g_{2}^2\\ &=\beta_{2}(1-\beta_{2})g_{1}^2+(1-\beta_{2})g_{2}^2\\ &=(1-\beta_{2})(\beta_{2}g_{1}^2+g_{2}^2)\\ &=(1-\beta_{2})(\beta_{2}^{2-1}g_{1}^2+\beta_{2}^{2-2}g_{2}^2)\\ &=(1-\beta_{2}){ extstyle \sum_{i=1}^{2}\beta_{2}^{2-i}g_{i}^2}\\ v_{t}&=(1-\beta_{2}){ extstyle \sum_{i=1}^{t}\beta_{2}^{t-i}g_{i}^2} \end{align*}

而我们实际上需要的是梯度的二阶矩估计，也就是E(g_{i}^{2})。因此使用动量求出来的二阶矩估计是有偏的，需要纠正。我们对动量二阶矩估计v_{t}求期望E(v_{t})，可以通过等比数列公式得到E(v_{t})与E(g_{i}^{2})的关系：?

\begin{align*} E(v_{t})&=(1-\beta_{2})E({ extstyle \sum_{i=1}^{t}\beta_{2}^{t-i}g_{i}^2})+\xi \\ &=(1-\beta_{2})(1+\beta_{2}^{1}+\beta_{2}^{2}+...+\beta_{2}^{t-1})E(g_{i}^2)+\xi \\ &=(1-\beta_{2})(\frac{1-(\beta_{2})^{t}}{1-\beta_{2}})E(g_{i}^2)+\xi \\ &=(1-\beta_{2}^{t})E(g_{i}^2)+\xi \end{align*}

因此，要得到E(g_{i}^{2})，就需要除掉前面的系数（(1-\beta_{2}^{t})是一个常数，\beta_{2}^{t}是贝塔2的t次方，t：t时刻）。

主要问题就是这些，其他的可以多看Adam之前一些优化器的资料，很多是一脉相承的。