前一篇说到LM优化算法。在介绍LM优化算法前，得先说说它是怎么一步步发展来的。因此，优化算法部分的介绍顺序是：梯度下降、牛顿法、高斯牛顿法、LM法。

一般待优化的目标函数都是由误差的平方和组成，也就是我们常见的最小二乘问题：

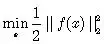
这里的 f 一般是非线性函数。我们在微积分课程里学过，如果想要求目标函数的极值（可能是极大值、极小值或者鞍点处的值），可以通过令目标函数的导数（如果可导）为零，求解析解得到。但是实际应用中函数 f 一般是非常复杂的非线性函数，没有解析解。所以一般最常用的优化方法就是迭代求解。

如何迭代呢？

以迭代求解极小值为例（如果求极大值，在前面加个负号转化为求极小值问题）。通用的方法就是先给定一个初值 θ0，对应目标函数值为 f(θ0)，这个初值可以是经验估计的或者随机指定（随机的话收敛会慢一些），然后我们改变（增大或减少） θ0 的值，得到一个新的值 θ1，如果 f(θ1)<f(θ0)，那么说明我们迭代的方向是朝着目标函数值减小的方向，离我们期待的极小值更近了一步，继续朝着这个方向改变 θ1的值，否则朝着相反的方向改变 θ1的值。如此循环迭代多次，直到达到终止条件结束迭代过程。这个终止条件可以是：相邻几次迭代的目标函数值差别在某个阈值范围内，也可以是达到了最大迭代次数等。我们认为迭代终止时的目标函数值就是极小值。

因此迭代的一般过程如下：

1、对于目标函数 f(x)，给定自变量某个初始值x0。这个初值可以是经验估计的或者随机指定。

2、根据采用的具体方法（梯度下降、牛顿、高斯牛顿、LM等）确定一个增量△xk

3、计算目标函数添加了增量后的值如下

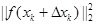
4、如果达到迭代终止条件（达到最大迭代次数或函数值/自变量变化非常小），则迭代结束，可以认为此时对应的目标函数值就是最小值。

5、如果没有达到迭代终止条件，按如下方式更新自变量，并返回第2步。

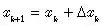
因此，不同的优化算法的不同主要体现在增量的更新方式上。如果采用不合适的更新方式，其实很容易陷入局部最小值。这里给出一个关于局部最小值和全局最小值的直观的理解。如下图所示：

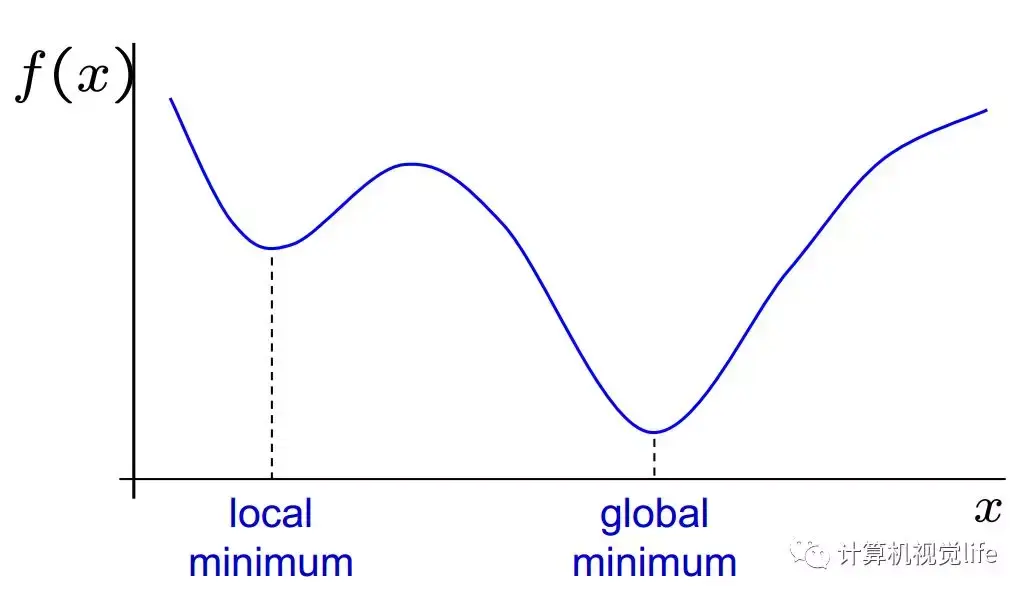
通常我们希望迭代得到的是全局最小值（只有一个）而不是局部最小值（可能有多个）。下图表示的是不同初始值对迭代结果的影响。如果我们初值设的是红色的θ0，最后找到的极小值位于 θ∞，在这个例子中它是全局最小值。但是如果我们初值设的是蓝色的 θ'0，最后我们找到的极小值位于 θ'∞，显然只是局部最小值，不是全局最小值。

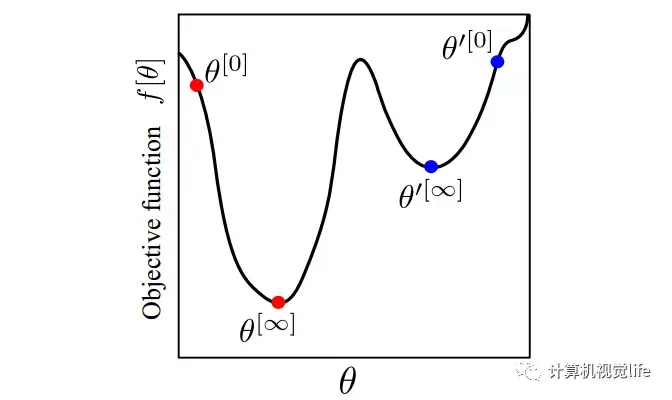
实际上按照上述迭代方法，很多时候我们找到的所谓「全局最小值」其实只是局部最小值，这并不是我们期望的。有没有保证局部最小值一定是全局最小值的情况呢？

答案是有，当然这就需要对目标函数有一定的限制。如果我们的目标函数是凸函数，那么可以保证最终找到的极小值就是最小值。很多人可能忘记了什么是凸函数，下面简单介绍一下。

凸函数（convex function）在优化算法中是一个非常重要的概念，其定义如下：

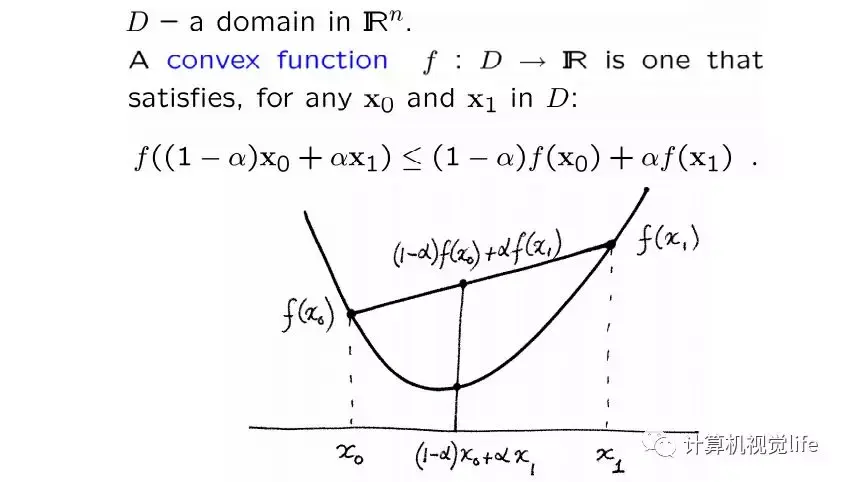
如果上面定义没有看懂也没关系，我们可以发现，凸函数其实就是一个「碗」状曲线，碗口向上。下图列举了几种凸函数和非凸函数的例子。如果一个函数是凸函数，那么它只有一个极小值点，也就是最小值点，从下图中也可以看出来。下图从左到右从上到下分别展示了：只有一个极小值的凸函数、只有一个极小值的非凸函数、有多个极值的非凸函数、加了噪音的非凸函数。

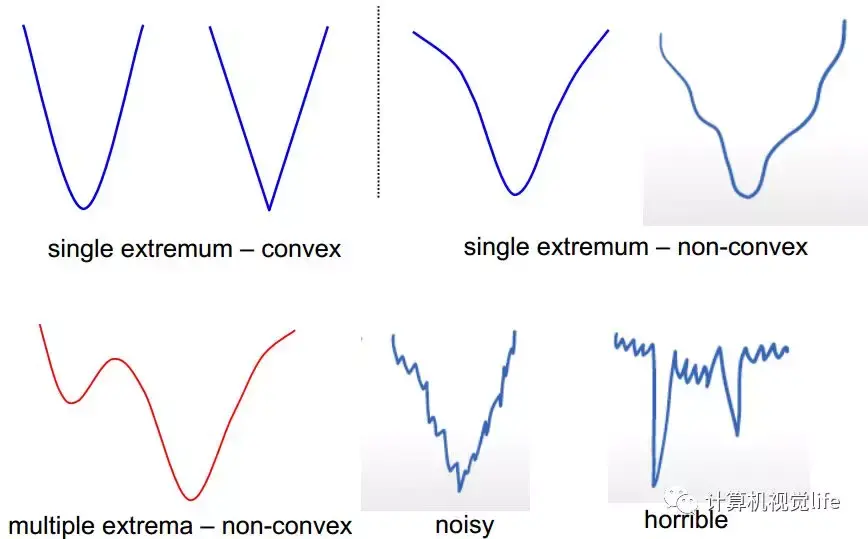
如何判断一个函数是否是凸函数？

对于一元二次可微函数，如果它的二阶导数是正的，那么该函数就是严格凸函数。对于多元二次可微函数，当它的Hessian矩阵（不懂没关系，后面会讲）是正定的时候，就是严格凸函数。好了，凸函数就介绍这么些，对凸函数做个总结吧。

1、如果一个函数是凸函数，那么它有且只有一个极值点，且这个极值点是最值点。

2、几个非负凸函数的和仍然是凸函数。

3、如果一个函数不是凸函数，那么它可能只有一个极值点，也可能有多个极值点（局部极值点和全局极值点）

凸函数讲完了，我们继续说说迭代求解最小值法。从最简单易懂的梯度下降法说起。

先来假设一个场景：一个人去探险被困在一座山上的某个位置，他必须赶在太阳下山之前回到山底的营地，否则会有危险。但是他对这座山不熟悉，而且视野有限无法看清哪里是山底，时间不多了，因此他必须采取比较激进的最快下山路线。由于可视距离有限，比如说10米。那么他需要以当前位置（坐标x0）为中心，以10米为半径寻找周围最陡峭的路（假设没有障碍），盯着这条10米长的路终点（坐标x1）走，当走到坐标为x1位置时，需要重新观察以当前位置为中心，以可视距离10米为半径区域重新寻找最陡峭的路，盯着这条路的终点（坐标x2）走，如此往复，那么最终他能够走到山底吗？

上述过程就是梯度下降法的实例。梯度下降法是求解无约束优化问题最简单和最古老的方法之一，虽然现在已经不具有实用性，但是许多有效算法都是以它为基础进行改进和修正而得到的。

梯度下降法，其本质是一阶优化算法，有时候也称为最速下降法（Steepest Descent）。与其对应的是梯度上升法(Gradient ascent)，用来求函数的极大值，两种方法原理一样，只是计算的过程中正负号不同而已。本文后续都是以梯度下降法为例进行介绍。

在微积分里，对函数求导数（如果是多元函数则求偏导）得到的就是梯度。具体来说，对于函数 f(x,y)， 在点 (x0,y0)，沿着梯度向量的方向就是(?f/?x0, ?f/?y0)，它的方向是 f(x,y) 增加最快的方向。或者说，沿着梯度向量的方向，更加容易找到函数的极大值。反过来说，沿着梯度向量相反的方向，也就是 -(?f/?x0, ?f/?y0) 的方向，梯度减少最快，也就是更加容易找到函数的极小值。

以一元函数为例，假设目标函数为F(x)，梯度的符号为?，那么在梯度下降中，自变量x每次按照如下方式迭代更新：

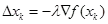
其中 λ 称为步长或者学习率。按照上述方式迭代更新自变量，直到满足迭代终止条件，此时认为自变量更新到函数最小值点。下图是梯度下降法的示意图。

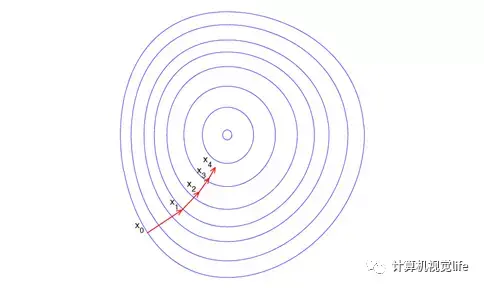
梯度下降法看起来很好，但是在具体使用过程中，会存在不少问题。

问题1：初始值选取

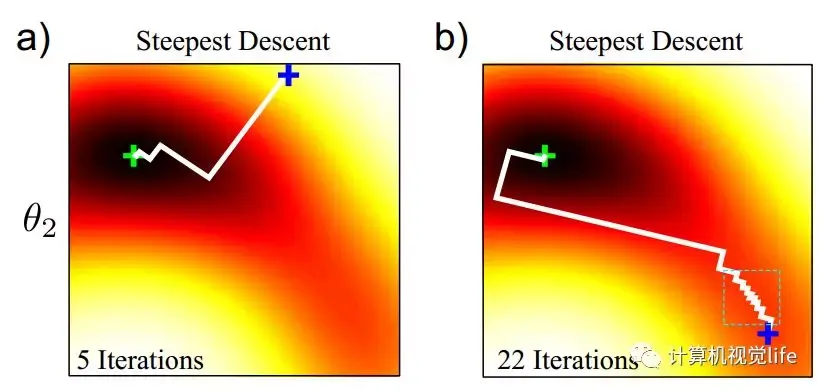
如下图所示，是二维函数优化的一个例子，不同颜色表示不同高度。我们初始值在蓝色的加号位置，最小值位于绿色的加号位置。图中展示了从不同的初始值开始迭代所需要的迭代次数，可以看到不同初始值会产生非常大的差异。(a) 图只经过5次迭代就收敛了， (b) 图经过了22次迭代才 收敛。

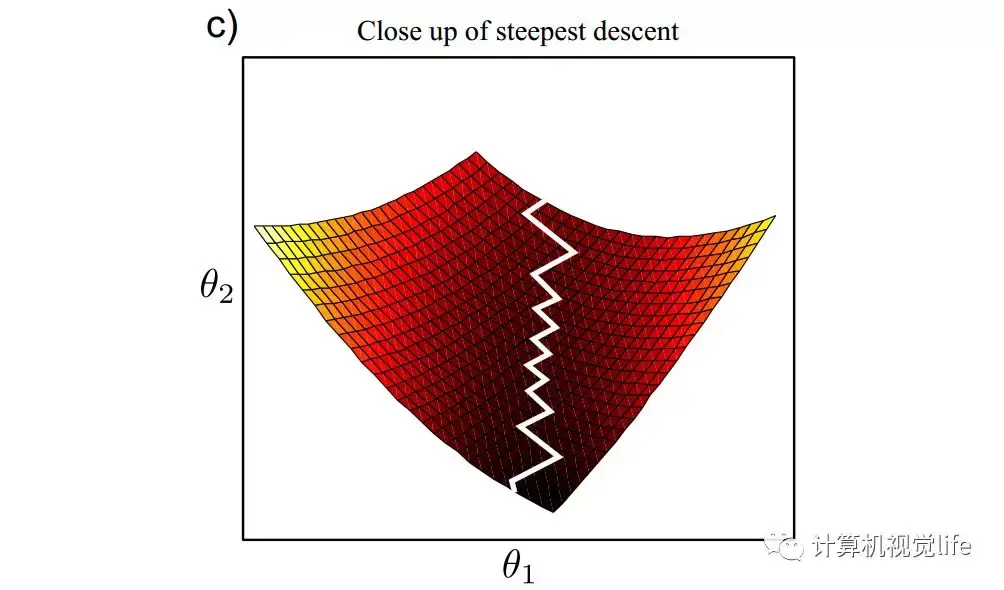
那么 (b)图里究竟为什么会多出那么多次的迭代呢？将局部细节放大后如下图所示，这部分「锯齿」状的震荡式下降是因为它经历了一个高度逐渐下降的「山谷」，而每次下降方向都与上一次垂直。换句话说，这种下降方式太「短视」，只关注了一个极小范围内的变化，而忽略了长远的趋势（牛顿法就是根据这点进行的改进，具体见后介绍），并不是一种「平滑」的下降。

既然初始值影响这么大，那么一般采用随机多次选取初始值进行多次迭代，然后将多次迭代结果进行比较，找出其中最小的那个作为最小值。这样会导致计算量急剧变大，最终确定的值也不能保证最小，并且因为随机选取，会导致每次最小值都不同，结果不稳定。

问题2：步长选取

步长，就是每一步走多远，这个参数如果设置的太大，那么很容易就在最小值附近徘徊；相反，如果设置的太小，则会导致收敛速度过慢。所以步长的选取也是一个非常关键的因素。

总结一下梯度下降法：

1、实际使用中使用梯度下降法找到的通常是局部极小值，而不是全局最小值。

2、具体找到的是哪个极小值和初始点位置有很大关系。

3、如果函数是凸函数，那么梯度下降法可以保证收敛到全局最优解（最小值）

4、梯度下降法收敛速度通常比较慢

5、梯度下降法中搜索步长 λ 很关键，步长太长会导致找不到极值点甚至震荡发散，步长太小收敛非常慢。

因此，前面的例子中，迷路的探险者可能花费了大量时间找到的却是一个假的山脚（山腰的某个低洼处，局部最小值）。

本文首发于公众号：计算机视觉life。原文链接：从零开始学习「张氏相机标定法」（四）优化算法前传